Qual é a melhor unidade de medida para ângulos — revoluções, graus ou radianos?
- revoluções
- Graus
- Radianos
- comparando revoluções, graus e radianos
- ensinar revoluções, graus e radianos acho que seria bom se os professores introduzissem revoluções (voltas) ao mesmo tempo em que introduzissem graus. Isso ajudará os alunos a entender os ângulos em um nível mais fundamental, menos dependente do número mágico arbitrário 360. Os professores já apresentamos o conceito geral de giros (liga) quando dizem coisas como “um círculo completo é de 360°”, mas eles podem tornar o conceito numericamente mais preciso, dizendo: “uma volta completa tem 360°, uma meia volta, é de 180°, um quarto de volta, é de 90°, e um oitavo sua vez, é de 45°” ou “escrita de 1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90°, e 1/8 rev = 45°”. Os alunos devem ocasionalmente praticar alguns cálculos usando revoluções (voltas) em vez de graus. Claro, os alunos precisarão gastar a maior parte do tempo aprendendo a calcular com graus (e mais tarde, radianos), porque esse é o padrão. ângulos em trigonometria e cálculo
revoluções
raramente aprendemos a usar a unidade de medida mais simples e natural para ângulos geométricos, a revolução (rev). Outros nomes para esta unidade são círculo completo, volta, volta completa e rotação (podridão). Estes são todos bons nomes e todos eles significam a mesma coisa.
1 círculo completo = 1 rev = 1 = 1 rot = 360°
Graus
No ensino fundamental, aprendemos que os ângulos são medidos em graus (°).
1 círculo completo = 360°
Radianos
Na escola, trigonometria e cálculo aulas, aprendemos que os matemáticos preferem radianos (rad).
1 círculo completo = 2π rad
Nota: Se você ainda não aprendeu sobre radianos na escola, você pode ignorar o radianos em tudo abaixo.
comparando revoluções, graus e radianos
vamos comparar revoluções e graus (e radianos).
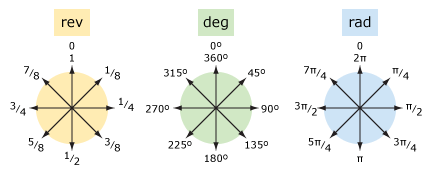
| palavras | ap | graus | rad |
|---|---|---|---|
| não vire | 0 | 0° | 0 |
| quarto de volta | 1/4 | 90° | π/2 |
| meia volta | 1/2 | 180° | π |
| três-quarto de volta | 3/4 | 270° | 3π/2 |
| turno completo | 1 | 360° | 2π |
| décimo segundo turno | 1/12 | 30° | π/6 |
| oitavo turno | 1/8 | 45° | π/4 |
| sexto turno | 1/6 | 60° | π/3 |
| quinto turno | 1/5 | 72° | 2π/5 |
| terceiro turno | 1/3 | 120° | 2π/3 |
| duas voltas | 2 | 720° | 4π |
| a três voltas | 3 | 1080° | 6π |
Para converter de revoluções em graus, multiplique por 360. Para converter de graus em revoluções, divida por 360.
quando você usa graus, costuma trabalhar com inteiros, mas quando usa revoluções (ou radianos), costuma trabalhar com frações (ou decimais). Os cálculos manuais às vezes são mais fáceis quando você usa revoluções, mas às vezes mais fáceis quando usa graus. É bom saber nos dois sentidos.Revoluções (voltas) são uma unidade de medida mais racional e natural do que Graus. Você terá uma compreensão mais profunda dos ângulos se pensar em revoluções em vez de graus. Um ângulo é mais fundamentalmente uma subdivisão de um círculo do que uma soma de graus. Por exemplo, um ângulo reto é mais fundamentalmente um quarto de círculo do que uma soma de 90 graus.
vamos dividir o círculo em n setores iguais (veja o diagrama abaixo). O ângulo de cada setor é 1 / n rev = 360 / n° = 2π / n rad. É mais fácil entender isso se você pensar em revoluções em vez de graus (ou radianos).

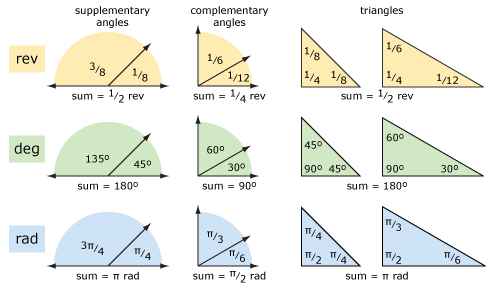
vejamos alguma geometria básica usando revoluções e graus (e radianos). O diagrama abaixo mostra ângulos suplementares, ângulos complementares e triângulos. Os conceitos são mais claros se você pensar em revoluções em vez de graus. A aritmética pode ser mais fácil usando graus se você tiver problemas para adicionar e subtrair frações.
vejamos os polígonos (veja o diagrama abaixo). Para um polígono regular com n lados, o ângulo externo é 1/n rev = 360/n° = 2π/n rad. É mais fácil entender isso se você pensar em revoluções em vez de graus (ou radianos). O ângulo interior é o complemento do ângulo exterior.

ensinar revoluções, graus e radianos acho que seria bom se os professores introduzissem revoluções (voltas) ao mesmo tempo em que introduzissem graus. Isso ajudará os alunos a entender os ângulos em um nível mais fundamental, menos dependente do número mágico arbitrário 360. Os professores já apresentamos o conceito geral de giros (liga) quando dizem coisas como “um círculo completo é de 360°”, mas eles podem tornar o conceito numericamente mais preciso, dizendo: “uma volta completa tem 360°, uma meia volta, é de 180°, um quarto de volta, é de 90°, e um oitavo sua vez, é de 45°” ou “escrita de 1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90°, e 1/8 rev = 45°”. Os alunos devem ocasionalmente praticar alguns cálculos usando revoluções (voltas) em vez de graus. Claro, os alunos precisarão gastar a maior parte do tempo aprendendo a calcular com graus (e mais tarde, radianos), porque esse é o padrão.
ângulos em trigonometria e cálculo
finalmente, vamos dar uma olhada rápida em matemática mais avançada: trigonometria e cálculo.
podemos considerar o uso de revoluções com funções trigonométricas (seno, cosseno, tangente). Por exemplo, em vez de dizer cos(60°) = 1/2 ou cos(π/3) = 1/2 usando radianos, podemos querer dizer cos(1/6) = 1/2 usando revoluções. Mas isso não é prático porque dependemos de calculadoras para avaliar as funções trigonométricas, e as calculadoras normalmente têm apenas modos DEG e RAD, não Modo Rev.
quando vamos para níveis mais profundos de matemática, como cálculo e Análise Matemática, verifica-se que os radianos são as unidades mais racionais e naturais. Por exemplo, considere esta equação fundamental: o limite do pecado(x)/x à medida que X se aproxima de 0 é exatamente 1. Esta equação não seria tão elegante se usássemos qualquer unidade que não seja radianos.