ANOVA Explicada por Exemplo,

plano de Fundo

Análise de variância, normalmente conhecida como ANOVA, é algo que, muitas vezes, encoberto em introdutório estatísticas de classes. Com a tecnologia de hoje, é fácil deixar o computador fazer todos os cálculos e apenas olhar para o valor p no final de uma mesa de aparência ocupada como a acima. Neste artigo, analisarei o que são esses números e o que ANOVA está realmente fazendo.

a ideia principal por trás da ANOVA é testar se há uma diferença estatisticamente significativa nas médias medidas entre subgrupos de uma amostra. O conceito remonta a cerca de 1920 com um estatístico britânico chamado Ronald Fisher, que estava analisando grandes quantidades de dados sobre o rendimento das culturas. Fisher usou ANOVA para provar que havia uma diferença significativa no peso médio das batatas quando diferentes fertilizantes foram usados.

para demonstrar a ANOVA nos dias atuais, vou analisar os preços do Vinho e não os pesos das batatas. Os dados para este exemplo são do conjunto de dados de revisão de vinhos da Kaggle, que contém milhares de avaliações sobre garrafas de vinho da WineEnthusiast. Eu filtrei para um subconjunto de 3.000 avaliações de vinhos dos Estados Unidos, Itália e França (1.000 por país) e usarei o ANOVA para testar se há uma diferença estatisticamente significativa no preço médio entre os países de origem.

um gráfico rápido da distribuição de preços por país mostra três distribuições bastante semelhantes, com a maioria dos preços em torno de US $25 por garrafa.

Tendo a média de cada país, vemos que a França tem a maior parte de vinhos caros, em média, seguida pela Itália e, finalmente, os EUA. Mas a questão é: esta é uma diferença genuína de preço entre os países ou isso poderia ser apenas devido à variação da amostra? É aqui que ANOVA entra em jogo.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

Os quatro passos para ANOVA são:

1. Formule uma hipótese
2. Defina um nível de significância
3. Calcule uma estatística F
4. Use a estatística F para derivar um valor p
5. Compare o valor de P E o nível de significância para decidir se deve ou não rejeitar a hipótese nula

formule uma hipótese

como acontece com quase todos os testes de significância estatística, ANOVA começa com a formulação de uma hipótese nula e alternativa. Para este exemplo, as hipóteses são as seguintes:

hipótese nula (H0): Não há diferença no preço médio do vinho entre os três países; eles são todos iguais. Hipótese alternativa( H1): o preço médio do vinho não é o mesmo entre os três países.

Nota, Este é um teste omnibus, o que significa que se formos capazes de rejeitar a hipótese nula, ela nos dirá que existe uma diferença estatisticamente significativa em algum lugar entre esses países, mas não nos dirá Onde está.

Defina um nível de significância

o nível de significância, ou alfa, é a probabilidade de rejeitar nossa hipótese nula quando ela realmente é verdadeira. Em outros termos, é a probabilidade de fazer um erro do tipo I.

normalmente, deve-se pesar os custos de fazer um erro Tipo I vs. A Tipo II para determinar o melhor alfa para um experimento, mas para este exemplo de brinquedo, vou usar o padrão .05 para o nosso Valor α.

calcule uma estatística F

a estatística F é simplesmente uma razão entre a variância entre as médias das amostras e a variância dentro das médias das amostras. Para este teste de ANOVA, veremos o quão longe o preço médio do vinho de cada país está do preço médio geral e dividiremos isso pela quantidade de variação no preço que existe na distribuição de amostras de cada país. A fórmula da estatística F está abaixo, o que pode parecer complicado até que a quebremos.

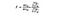
SSB = Soma dos quadrados entre os grupos. Esta é a soma da diferença quadrada entre a média de cada grupo e a média geral vezes o número de elementos por grupo. Para este exemplo, tomamos a média do preço do vinho de cada país, subtraímos da média geral, quadramos a diferença e multiplicamos por 1.000 (o número de pontos de dados por país).

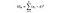
SSW = Soma de quadrados dentro dos grupos. Esta é a soma da diferença quadrada entre a média do grupo e cada valor no grupo. Para a França, tomaríamos o preço médio do vinho francês, subtrairíamos e quadraríamos a diferença para cada garrafa de vinho francês dos mil pontos de dados desse grupo.

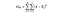
DoFB = Graus de liberdade entre os grupos, simplesmente, o número de grupos menos 1. Temos três países diferentes que estamos comparando, então os graus de liberdade aqui são 2.
DoFW = graus de liberdade dentro dos grupos, simplesmente o número de pontos de dados menos o número de grupos. Temos 3.000 pontos de dados e três países diferentes, então isso é 2.997 para este exemplo.

dividir a soma dos quadrados para um grupo por seus graus de liberdade produz os quadrados médios para esse grupo, e a estatística F é apenas uma proporção dos quadrados médios entre os quadrados médios dentro.

abaixo, calculo manualmente esses valores em Python e acabo com uma estatística F de ~4,07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

usando a estatística F, calcule um valor p

uma vez que tenhamos nossa estatística F, Nós a conectamos a uma distribuição F para obter um valor p. Você pode encontrar uma tabela para esses valores na parte de trás de qualquer livro de estatísticas ou há calculadoras on-line muito mais fáceis que farão isso por você. Com nossos graus específicos de liberdade, uma estatística F de 4,07 produz um valor p .0172.

Comparar o valor de p e o nível de significância para decidir se quer ou não rejeitar a hipótese nula

Nossos p-valor significa que, supondo que a hipótese nula (todos os países têm a mesma média de preço do vinho) é verdadeira, há cerca de um 1.7% de chance de ver os dados que temos por pura chance de amostragem. Ao definir nosso nível de significância, ou alfa, em 5% antes de tudo isso, dissemos que estaríamos dispostos a aceitar uma chance de 5% de rejeitar o nulo quando for verdade. Como nosso valor p está abaixo do nosso nível de significância pré-determinado, podemos rejeitar a hipótese nula e dizer que há uma diferença estatisticamente significativa no preço médio do vinho entre os países.

lembre-se que a ANOVA é um teste omnibus, ou seja, porque somos capazes de rejeitar o nulo sabemos que existe uma diferença entre os preços médios do vinho entre os países, mas não exatamente onde. Para descobrir onde está a diferença, realizaríamos testes de hipóteses entre dois países de cada vez.

ANOVA automática

como com a maioria das coisas na vida, Python tem uma solução intuitiva para conduzir ANOVA com a biblioteca statsmodel. O código abaixo faz todos os cálculos neste artigo e produz uma tabela de resumo completa com uma estatística F e valor p.

Obrigado pela leitura, código completo e os dados podem ser encontrados na minha página do GitHub.