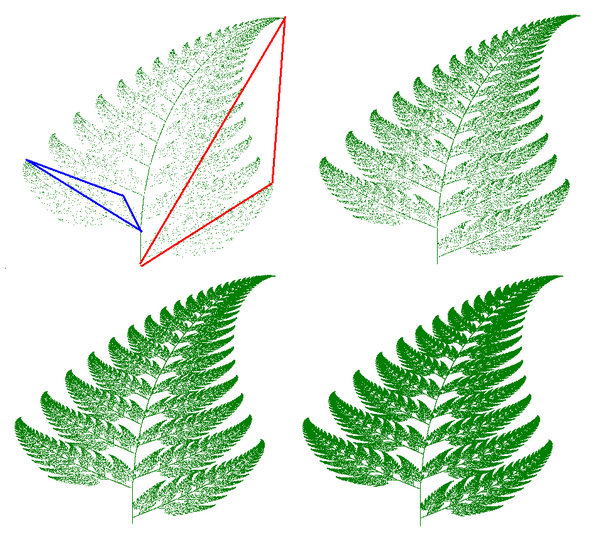
프랙탈 아트는 예술과 수학의 동맹을 나타냅니다. 이 최근의 예술 형식은 컴퓨터를 사용하여 수학 공식에서 이미지를 만듭니다. 프랙탈 아트는 종종 기하학적 모양,복잡한 패턴 및 풍부한 세부 사항을 가지고 있습니다. 그러나 수학 공식에서 이미지를 만드는 방법은 무엇입니까?
우선,”프랙탈”은 무엇을 의미합니까?
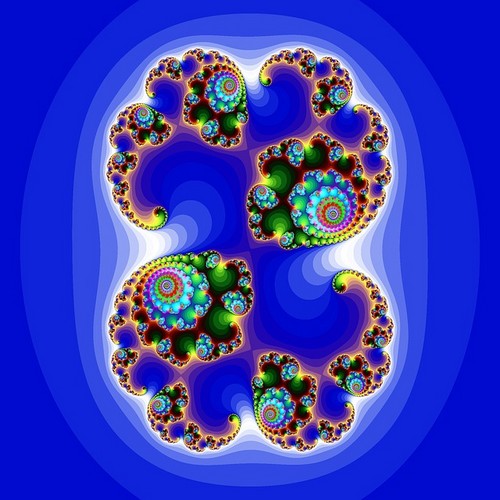
1970 년대에 컴퓨터 과학자 벤와 만델브로트는 가장 유명한 프랙탈 이미지 중 하나인 만델브로트를 발견했다.

이 발견은 컴퓨터 개발,특히 컴퓨팅 성능 덕분에 가능합니다. 그것은 또한 역동적 인 현상(난류,유체의 소용돌이,진동,구름 모양 등)을 연구하는 혼돈 이론의 발전의 과학적 맥락에서 일어난다.).
마찬가지로 프랙탈 기하학은 복잡한 윤곽(눈송이,나무의 잎,구름 모양,소용돌이,혈액 네트워크의 수목,해상 해안의 모양 등)을 가진 자연의 모양에서 발견됩니다.)그것은 이해하기 어려운 것을,그리고 이전의 수학적 도구를 모델링 할 수 있습니다.

프랙탈 이미지의 특성
프랙탈 차원
용어”프랙탈”은 비 전체,분수 차원의 아이디어를 의미한다. 1960 년대까지 수학은 정수 치수를 사용하여 분해 가능한 물체를 연구했습니다:
점:치수 0
선:치수 1
계획:치수 2
볼륨:치수 3
그러나 종이 한 장을 상상해보십시오. 그것은 평면을 나타내므로 2 와 같은 차원이 있습니다. 이 시트를 구겨 내면 이제 볼륨(치수 3)을 차지하지만 구겨진 시트를 컨테이너를 채우는 것처럼 재료로”채울”수 없기 때문에 볼륨이 아닙니다. 따라서 구겨진 시트의 치수는 예를 들어 2 에서 3:2.568 사이입니다. 프랙탈 차원! 따라서 프랙탈 개체는 복잡하고 불규칙한 모양을 가지며 윤곽선이 접 히고 접 힙니다.
자기 유사성
복잡성에도 불구하고 프랙탈 객체는 유사한 세부 사항을 나타낸다. 프랙탈 내부를 확대하면 동일한 전체 패턴이 다른 스케일에서 반복되고 무한대로 반복됩니다. 따라서 한 부분은 전체와 비슷합니다. 이 속성을 스케일 불변성이라고합니다.

유형학
재발에 의한 도형

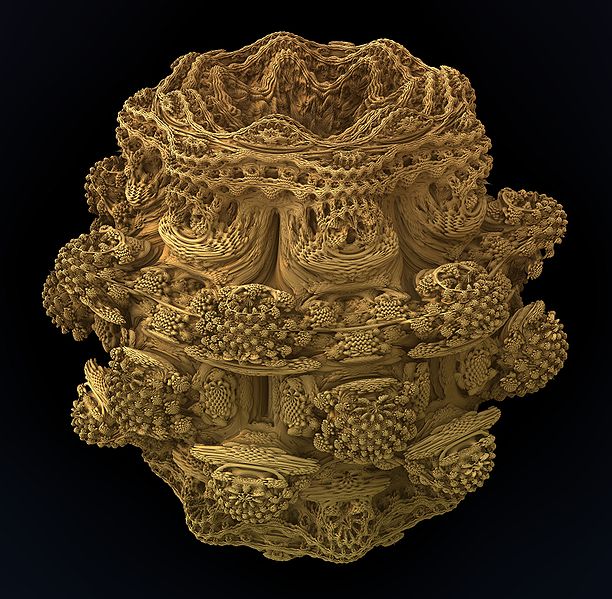
반복 함수 시스템



프랙탈 이미지의 생성,”단순성은 복잡성을 낳는다”
프랙탈 이미지의 구성은 루프에서 실행되는 알고리즘의 사용을 기반으로합니다. 그것은 일련의 간단한 작업을 반복하는 반복적 인 프로세스입니다.
반복에 의한 도형
공간의 각 점에 대해 점의 좌표가 방정식으로 전달됩니다. 결과는 동일한 방정식으로 그 때 다시 먹입니다. 작업은 여러 번 연속으로 수행됩니다(반복). 그런 다음 결과를 테스트합니다. 결과가 무한대 경향이 있다면,시작점은 전체에없는:그것은 흰색으로 표시됩니다. 결과가 안정적이거나 주기적으로 유지되면 시작점은 전체에 있습니다.이 점은 검은 색입니다. 경계에 있는 점의 경우 집합에 있는지 외부에 있는지 확인하는 것이 더 어렵습니다. 그런 다음 더 많은 반복을 수행 할 필요가 있습니다. 점을 결정하는 데 필요한 반복 횟수에 따라 다른 음영으로 색상이 지정됩니다. 이 경계의 포인트는 프랙탈에게 복잡하고 얽힌 모양을 제공합니다.
만델브로트 세트를 그리려면 각 픽셀이 평면에서 나타내는 복소수를 사용합니다. 각 점에 대해 다음 방정식을 실행합니다.
반복 함수 시스템
이미지 구성은 여기에서 자체 복사를 통해 수행됩니다. 그러나 각 복사본에서 복사 된 이미지는 기하학적 변환(선형 함수로 수학에서 표현되는 선형 변환)을 거칩니다. 이러한 변환은 회전,평탄화,전단 등이 될 수 있으며 복사본도 원본 이미지에 다시 배치되기 전에 축소됩니다. 이 과정은 이미지가 형성 될 때까지 반복됩니다.
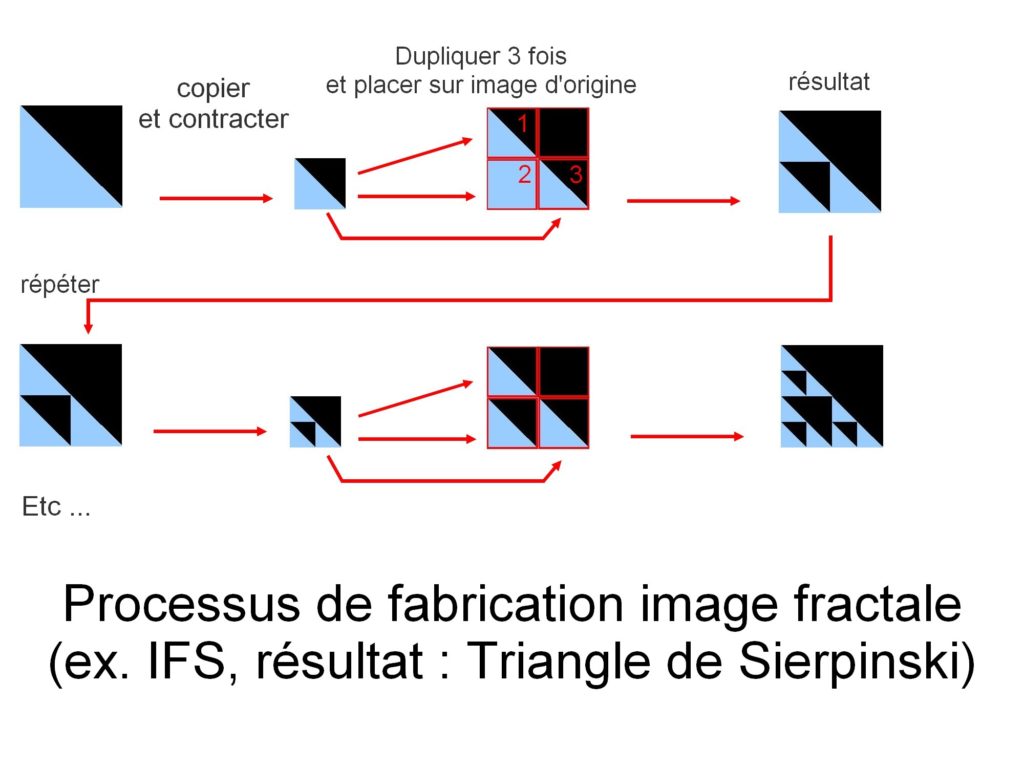
이 예제에서는 시에르핀스키 삼각형의 이미지가 생성됩니다.
또 다른 예는 코흐 눈송이의 생성이다.

나무,양치류 등과 같은 자연 물체를 연상시키는 이미지를 쉽게 생성 할 수 있습니다.