ANOVA Expliquée par Exemple

Contexte

L’analyse de la variance, généralement appelée ANOVA, est souvent passée sous silence dans les classes de statistiques d’introduction. Avec la technologie d’aujourd’hui, il est facile de laisser l’ordinateur faire tous les calculs et de simplement regarder la valeur p à la fin d’un tableau occupé comme celui ci-dessus. Dans cet article, je vais passer en revue ce que sont ces chiffres et ce que fait réellement ANOVA.

L’idée principale derrière l’ANOVA est de tester s’il existe une différence statistiquement significative dans les moyennes mesurées entre les sous-groupes d’un échantillon. Le concept remonte à environ 1920 avec un statisticien britannique du nom de Ronald Fisher, qui analysait des quantités massives de données sur les rendements des cultures. Fisher a utilisé ANOVA pour prouver qu’il y avait une différence significative dans le poids moyen des pommes de terre lorsque différents engrais étaient utilisés.

Pour démontrer l’ANOVA de nos jours, je regarderai les prix du vin plutôt que le poids des pommes de terre. Les données de cet exemple proviennent du jeu de données Wine Review de Kaggle, qui contient des milliers d’avis sur des bouteilles de vin de WineEnthusiast. Je l’ai filtré jusqu’à un sous-ensemble de 3 000 critiques de vins des États-Unis, d’Italie et de France (1 000 par pays) et j’utiliserai ANOVA pour tester s’il existe une différence statistiquement significative dans le prix moyen entre les pays d’origine.

Un graphique rapide de la distribution des prix par pays montre trois distributions assez similaires, avec la majorité des prix autour de 25 a la bouteille.

En prenant la moyenne de chaque pays, on voit que la France a le vin le plus cher en moyenne, suivie de l’Italie puis enfin des États-Unis. Mais la question est la suivante: s’agit-il d’une véritable différence de prix entre les pays ou cela pourrait-il simplement être dû à une variation de l’échantillon? C’est là qu’ANOVA entre en jeu.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

Les quatre étapes de l’ANOVA sont:

1. Formuler une hypothèse
2. Définissez un niveau de signification
3. Calculer une statistique F
4. Utilisez la statistique F pour dériver une valeur p
5. Comparez la valeur p et le niveau de signification pour décider de rejeter ou non l’hypothèse nulle

Formuler une hypothèse

Comme pour presque tous les tests de signification statistique, ANOVA commence par formuler une hypothèse nulle et alternative. Pour cet exemple, les hypothèses sont les suivantes:

Hypothèse nulle (H0): Il n’y a pas de différence dans le prix moyen du vin entre les trois pays; ils sont tous les mêmes.
Hypothèse alternative (H1) : Le prix moyen du vin n’est pas le même entre les trois pays.

Notez qu’il s’agit d’un test omnibus, ce qui signifie que si nous sommes en mesure de rejeter l’hypothèse nulle, cela nous indiquera qu’une différence statistiquement significative existe quelque part entre ces pays, mais cela ne nous dira pas où elle se trouve.

Définir un niveau de signification

Le niveau de signification, ou alpha, est la probabilité de rejeter notre hypothèse nulle lorsqu’elle est réellement vraie. En d’autres termes, c’est la probabilité de faire une erreur de type I.

En règle générale, il faut peser les coûts d’une erreur de type I par rapport à une erreur de type II pour déterminer le meilleur alpha pour une expérience, mais pour cet exemple de jouet, je vais simplement utiliser la norme.05 pour notre valeur α.

Calculer une statistique F

La statistique F est simplement un rapport entre la variance entre les moyennes d’échantillons et la variance dans les moyennes d’échantillons. Pour ce test ANOVA, nous examinerons la distance entre le prix moyen du vin de chaque pays et le prix moyen global, et nous le diviserons par la variation du prix dans la distribution de l’échantillon de chaque pays. La formule de la statistique F est ci-dessous, ce qui peut sembler compliqué jusqu’à ce que nous la décomposions.

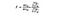
SSB = Somme des carrés entre les groupes. Il s’agit de la somme de la différence au carré entre la moyenne de chaque groupe et la moyenne globale fois le nombre d’éléments par groupe. Pour cet exemple, nous prenons la moyenne du prix du vin de chaque pays, la soustrayons de la moyenne globale, plaçons la différence et multiplions par 1 000 (le nombre de points de données par pays).

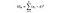
SSW = Somme des carrés dans les groupes. Il s’agit de la somme de la différence au carré entre la moyenne du groupe et chaque valeur du groupe. Pour la France, nous prendrions le prix moyen du vin français, puis soustrayions et équarririons la différence pour chaque bouteille de vin français des mille points de données de ce groupe.

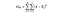
DoFB = Degrés de liberté entre les groupes, simplement le nombre de groupes moins 1. Nous avons trois pays différents que nous comparons, donc les degrés de liberté ici sont de 2.
DoFW = Degrés de liberté au sein des groupes, simplement le nombre de points de données moins le nombre de groupes. Nous avons 3 000 points de données et trois pays différents, c’est donc 2 997 pour cet exemple.

En divisant la somme des carrés d’un groupe par ses degrés de liberté, on obtient les carrés moyens pour ce groupe, et la statistique F n’est qu’un rapport des carrés moyens entre sur les carrés moyens à l’intérieur.

Ci-dessous, je calcule manuellement ces valeurs en Python et je me retrouve avec une statistique F de ~ 4,07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

En utilisant la statistique F, calculez une valeur p

Une fois que nous avons notre statistique F, nous la connectons à une distribution F pour obtenir une valeur p. Vous pouvez trouver un tableau pour ces valeurs au dos de n’importe quel livre de statistiques ou il existe des calculatrices en ligne beaucoup plus faciles qui le feront pour vous. Avec nos degrés de liberté spécifiques, une statistique F de 4,07 donne une valeur p.0172.

Comparez la valeur p et le niveau de signification pour décider de rejeter ou non l’hypothèse nulle

Notre valeur p signifie qu’en supposant que l’hypothèse nulle (tous les pays ont le même prix moyen du vin) est vraie, il y a à peu près un 1.7% de chances de voir les données que nous avons par simple chance d’échantillonnage. En fixant notre niveau de signification, ou alpha, à 5% avant tout cela, nous avons dit que nous serions prêts à accepter une chance de 5% de rejeter le nul quand il est vrai. Puisque notre valeur p est inférieure à notre niveau de signification prédéterminé, nous pouvons rejeter l’hypothèse nulle et dire qu’il existe une différence statistiquement significative du prix moyen du vin entre les pays.

Rappelez-vous que l’ANOVA est un test omnibus, ce qui signifie que parce que nous sommes capables de rejeter le nul, nous savons qu’il existe une différence entre les prix moyens des vins entre les pays, mais pas exactement où. Pour trouver où se situe la différence, nous effectuerions ensuite des tests d’hypothèse entre deux pays à la fois.

ANOVA automatique

Comme pour la plupart des choses de la vie, Python dispose d’une solution intuitive pour effectuer une ANOVA avec la bibliothèque statsmodel. Le code ci-dessous effectue tous les calculs de cet article et génère un tableau récapitulatif complet avec une statistique F et une valeur p.

Merci d’avoir lu, le code complet et les données peuvent être trouvés sur ma page GitHub.