Quelle est la meilleure unité de mesure pour les angles – révolutions, degrés ou radians?
Révolutions
Nous apprenons rarement à utiliser l’unité de mesure la plus simple et la plus naturelle pour les angles géométriques, la révolution (rev). Les autres noms de cette unité sont cercle complet, tour, tour complet et rotation (pourriture). Ce sont tous de bons noms et ils signifient tous la même chose.
1 cercle complet = 1 tour = 1 tour = 1 pourriture = 360°
Degrés
À l’école primaire, on apprend que les angles sont mesurés en degrés (°).
1 cercle complet = 360°
Radians
Dans les cours de trigonométrie et de calcul du lycée, nous apprenons que les mathématiciens préfèrent les radians (rad).
1 cercle complet = 2π rad
Remarque: Si vous n’avez pas encore appris les radians à l’école, vous pouvez ignorer les radians dans tout ce qui suit.
Comparaison des révolutions, des degrés et des Radians
Comparons les révolutions et les degrés (et les radians).
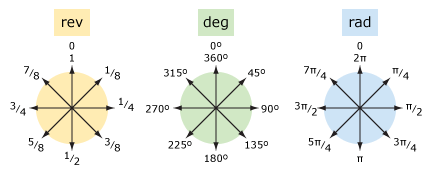
| mots | rev | deg | rad |
|---|---|---|---|
| pas de tour | 0 | 0° | 0 |
| quart de tour | 1/4 | 90° | π/2 |
| demi-tour | 1/2 | 180° | π |
| trois quarts de tour | 3/4 | 270° | 3π/2 |
| tour complet | 1 | 360° | 2π |
| douzième tour | 1/12 | 30° | π/6 |
| huitième tour | 1/8 | 45° | π/4 |
| sixième tour | 1/6 | 60° | π/3 |
| cinquième tour | 1/5 | 72° | 2π/5 |
| troisième tour | 1/3 | 120° | 2π/3 |
| deux tours | 2 | 720° | 4π |
| trois tours | 3 | 1080° | 6π |
Pour convertir des révolutions en degrés, multipliez par 360. Pour convertir des degrés en révolutions, divisez par 360.
Lorsque vous utilisez des degrés, vous travaillez souvent avec des entiers, mais lorsque vous utilisez des révolutions (ou des radians), vous travaillez souvent avec des fractions (ou des décimales). Les calculs manuels sont parfois plus faciles lorsque vous utilisez des révolutions, mais parfois plus faciles lorsque vous utilisez des degrés. Il est bon de savoir dans les deux sens.
Les révolutions (tours) sont une unité de mesure plus rationnelle et naturelle que les degrés. Vous comprendrez mieux les angles si vous pensez aux révolutions plutôt qu’aux degrés. Un angle est plus fondamentalement une subdivision d’un cercle plutôt qu’une somme de degrés. Par exemple, un angle droit est plus fondamentalement un quart de cercle plutôt qu’une somme de 90 degrés.
Divisons le cercle en n secteurs égaux (voir diagramme ci-dessous). L’angle de chaque secteur est de 1/n rev = 360/n° = 2π/n rad. Il est plus facile de comprendre cela si vous pensez aux révolutions plutôt qu’aux degrés (ou radians).

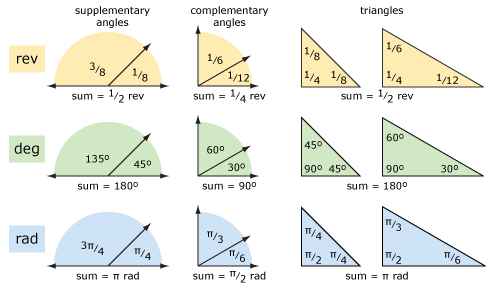
Regardons une géométrie de base en utilisant des révolutions et des degrés (et des radians). Le diagramme ci-dessous montre les angles supplémentaires, les angles complémentaires et les triangles. Les concepts sont plus clairs si vous pensez aux révolutions plutôt qu’aux degrés. L’arithmétique peut être plus facile en utilisant des degrés si vous avez du mal à ajouter et à soustraire des fractions.
Regardons les polygones (voir le diagramme ci-dessous). Pour un polygone régulier à n côtés, l’angle extérieur est de 1/n rev = 360/n° = 2π/n rad. Il est plus facile de comprendre cela si vous pensez aux révolutions plutôt qu’aux degrés (ou radians). L’angle intérieur est le complément de l’angle extérieur.

Enseigner les révolutions, les degrés et les Radians
Je pense qu’il serait bon que les enseignants introduisent des révolutions (tours) en même temps qu’ils introduisent des degrés. Cela aidera les élèves à comprendre les angles à un niveau plus fondamental, moins dépendant du nombre magique arbitraire 360. Les enseignants introduisent déjà le concept général de tours (tours) lorsqu’ils disent des choses comme « un cercle complet vaut 360 ° », mais ils peuvent rendre le concept plus précis numériquement en disant « un tour complet vaut 360 °, un demi-tour vaut 180 °, un quart de tour vaut 90 ° et un huitième tour vaut 45 ° » ou en écrivant « 1 tour = 360 °, 1/2 tour = 180 °, 1/4 tour = 90 ° et 1/8 tour = 45 ° ». Les étudiants devraient parfois s’entraîner à faire quelques calculs en utilisant des révolutions (tours) plutôt que des degrés. Bien sûr, les étudiants devront passer la plupart de leur temps à apprendre à calculer avec des degrés (et plus tard, des radians), car c’est la norme.
Angles en trigonométrie et Calcul
Enfin, jetons un coup d’œil aux mathématiques plus avancées: trigonométrie et calcul.
On peut envisager d’utiliser des révolutions avec des fonctions trigonométriques (sinus, cosinus, tangente). Par exemple, au lieu de dire cos(60 °) = 1/2 ou cos(π / 3) = 1/2 en utilisant des radians, nous pourrions vouloir dire cos(1/6) = 1/2 en utilisant des révolutions. Mais ce n’est pas pratique car nous dépendons des calculatrices pour évaluer les fonctions trigonométriques, et les calculatrices n’ont généralement que les modes DEG et RAD, pas le mode REV.
Lorsque nous passons à des niveaux plus profonds de mathématiques, tels que le calcul et l’analyse mathématique, il s’avère que les radians sont les unités les plus rationnelles et les plus naturelles. Par exemple, considérons cette équation fondamentale: la limite de sin(x) / x lorsque x s’approche de 0 est exactement 1. Cette équation ne serait pas si élégante si nous utilisions une unité autre que les radians.