El arte fractal representa la alianza entre arte y matemáticas. Esta forma de arte reciente utiliza computadoras para crear imágenes a partir de fórmulas matemáticas. El arte fractal tiene una apariencia a menudo geométrica, patrones intrincados y una gran cantidad de detalles. Pero, ¿cómo crear imágenes a partir de fórmulas matemáticas ?
- En primer lugar, ¿qué significa «Fractal»?
- Características de las imágenes fractales
- La dimensión fractal
- Auto-similitud
- Tipología
- Fractales por recurrencia
- IFS, sistemas de funciones iteradas
- Generación de imágenes fractales,»La simplicidad genera complejidad»
- Fractales por recurrencia
- IFS, sistemas de funciones iteradas
En primer lugar, ¿qué significa «Fractal»?
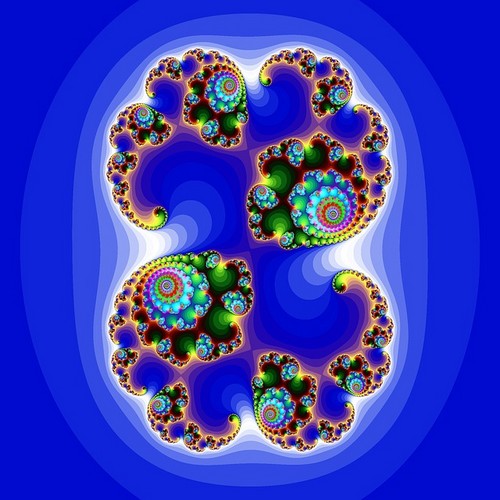
En la década de 1970, el científico informático Benoit Mandelbrot descubrió una de las imágenes fractales más famosas: el conjunto Mandelbrot.

Este descubrimiento es posible gracias al desarrollo de la computadora, en particular gracias a la potencia de cálculo. También tiene lugar en el contexto científico del desarrollo de la teoría del Caos que estudia los fenómenos dinámicos (turbulencia, vórtices en un fluido, oscilación, forma de nube, etc.).).
Asimismo, la geometría fractal se encuentra en las formas de la naturaleza con contornos complejos (copo de nieve, hoja de un árbol, forma de nubes, remolinos, arborescencia de la red de sangre, forma de costas marítimas, etc.) que era difícil de entender, y de modelar con las herramientas matemáticas anteriores.

Características de las imágenes fractales
La dimensión fractal
El término «fractal» se refiere a la idea de una dimensión fraccionaria no integral. Hasta la década de 1960, estudió matemáticas descomponible objetos utilizando entero dimensiones:
un punto: dimensión 0
una línea: dimensión 1
un plan: dimensión 2
volumen: dimensión 3
Pero imagino que una hoja de papel. Representa un plano, por lo tanto, tiene una dimensión igual a 2. Si arrugamos esta hoja, ahora ocupa un volumen (dimensión 3), pero no es un volumen porque no podemos «llenar» la hoja arrugada con un material como se llenaría un recipiente. Por lo tanto, la dimensión de la hoja arrugada está entre 2 y 3 : 2.568, por ejemplo. Una dimensión fractal ! Por lo tanto, los objetos fractales tienen formas complejas e irregulares, con contornos plegados y plegados sobre sí mismos.
Auto-similitud
A pesar de su complejidad, un objeto fractal exhibe detalles similares. El zoom dentro de un fractal muestra el mismo patrón general repetido a diferentes escalas y hasta el infinito. Por lo tanto, una parte es similar al todo. Esta propiedad se llama invariancia de escala.

Tipología
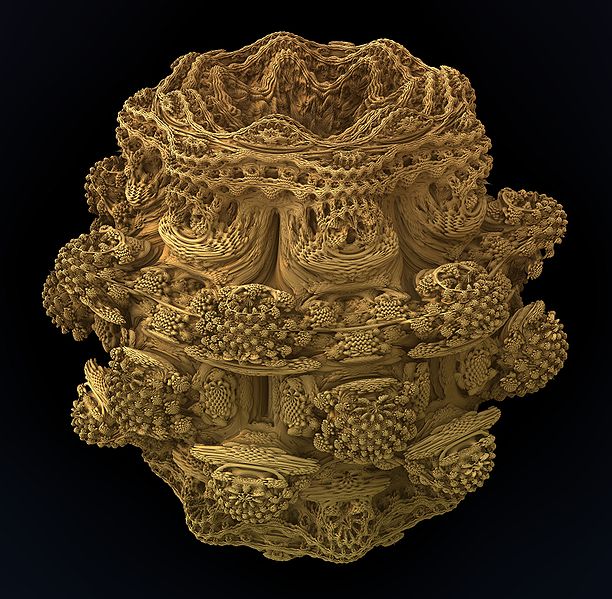
Fractales por recurrencia

IFS, sistemas de funciones iteradas



Generación de imágenes fractales,»La simplicidad genera complejidad»
La construcción de imágenes fractales se basa en el uso de Algoritmos ejecutados en bucle. Es un proceso iterativo que repite una serie de operaciones simples.
Fractales por recurrencia
Para cada punto en el espacio, las coordenadas del punto se pasan a una ecuación. El resultado se devuelve a la misma ecuación. La operación se realiza varias veces seguidas (iteraciones). Luego probamos el resultado. Si el resultado tiende al infinito, entonces el punto de partida no está en el todo : es de color blanco. Si el resultado se mantiene estable, o periódico, entonces el punto de partida está en el todo : es de color negro. Para los puntos en el límite, es más difícil determinar si están en el conjunto o en el exterior. Entonces es necesario realizar más iteraciones. Dependiendo del número de iteraciones necesarias para determinar el punto, se colorea en diferentes tonos. Los puntos de este borde dan al fractal su aspecto complicado y enredado.
Para dibujar el conjunto de Mandelbrot, usamos números complejos que representan cada uno un píxel en el plano. Ejecutamos la siguiente ecuación para cada punto: Zn + 1 = Zn2 + C, con Z0 = 0.
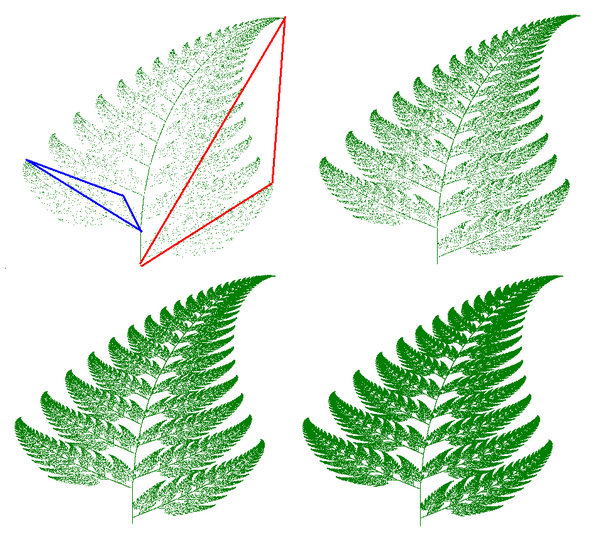
IFS, sistemas de funciones iteradas
La construcción de imágenes se realiza aquí copiándose a sí misma. Pero con cada copia, la imagen copiada sufre una transformación geométrica (una transformación lineal representada en matemáticas por una función lineal). Estas transformaciones pueden ser rotaciones, aplanamiento, corte The Las copias también se contraen antes de volver a colocarse en la imagen original. El proceso se repite hasta que se forma una imagen.
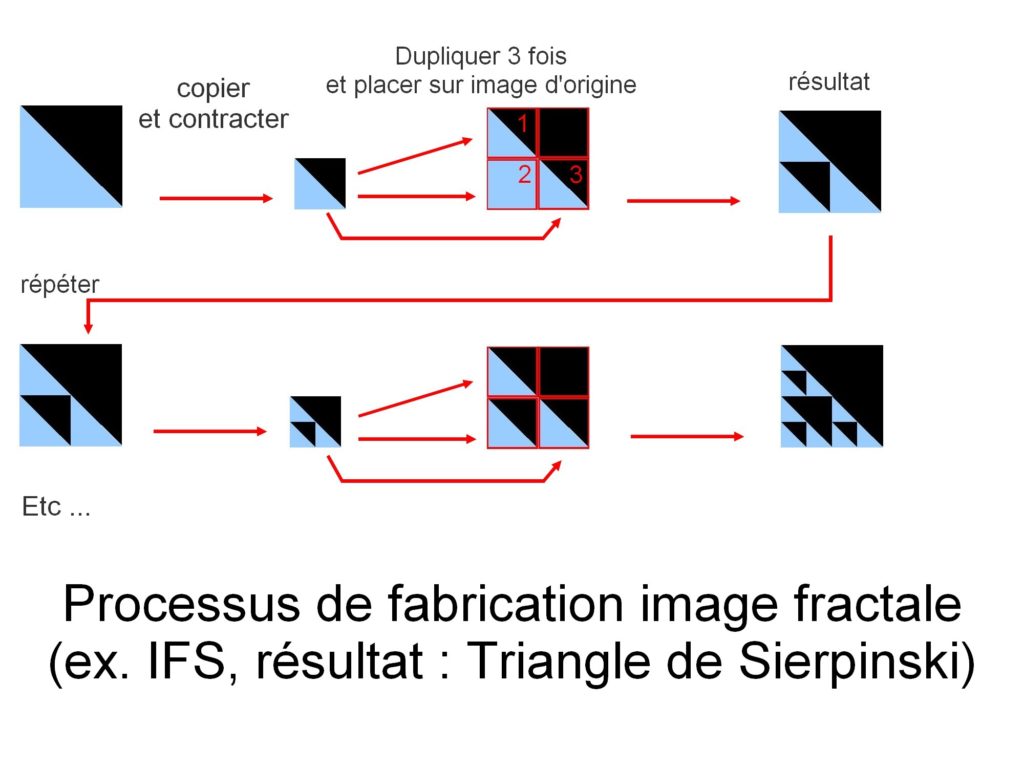
Este ejemplo da como resultado la imagen del triángulo de Sierpinski.
Otro ejemplo es la generación del copo de nieve Koch.

IFS puede producir fácilmente imágenes que recuerdan a objetos naturales,como árboles, helechos, etc.