Cálculo manual de una tabla ANOVA con Python
Fondo

El análisis de varianza, normalmente conocido como ANOVA, es algo que a menudo se pasa por alto en las clases introductorias de estadística. Con la tecnología actual, es fácil dejar que la computadora haga todos los cálculos y simplemente mirar el valor p al final de una tabla de aspecto ocupado como la de arriba. En este artículo, repasaré cuáles son estos números y qué está haciendo ANOVA en realidad.
La idea principal detrás de ANOVA es probar si hay una diferencia estadísticamente significativa en las medias medidas entre los subgrupos de una muestra. El concepto se remonta a alrededor de 1920 con un estadístico británico llamado Ronald Fisher, que estaba analizando cantidades masivas de datos sobre el rendimiento de los cultivos. Fisher usó ANOVA para demostrar que había una diferencia significativa en el peso promedio de las papas cuando se usaron diferentes fertilizantes.
Para demostrar ANOVA en la actualidad, estaré mirando los precios del vino en lugar de los pesos de las papas. Los datos de este ejemplo provienen del conjunto de datos de revisión de vinos de Kaggle, que contiene miles de reseñas sobre botellas de vino de WineEnthusiast. Lo he filtrado a un subconjunto de 3,000 reseñas de vinos de Estados Unidos, Italia y Francia (1,000 por país) y usaré ANOVA para probar si hay una diferencia estadísticamente significativa en el precio promedio entre los países de origen.
Un gráfico rápido de la distribución de precios por país muestra tres distribuciones bastante similares, con la mayoría de los precios alrededor de 2 25 por botella.

se Toma la media de cada país, podemos ver que Francia tiene el vino más caro, en promedio, seguido por Italia y, finalmente, la de NOSOTROS. Pero la pregunta es, ¿se trata de una diferencia genuina en el precio entre países o podría deberse simplemente a la variación de la muestra? Aquí es donde ANOVA entra en juego.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
Los cuatro pasos para ANOVA son:
1. Formular una hipótesis
2. Establecer un nivel de significación
3. Calcular una estadística F
4. Utilice la estadística F para obtener un valor p
5. Comparar el valor p y el nivel de significación para decidir si rechazar o no la hipótesis nula
Formular una hipótesis
Al igual que con casi todas las pruebas de significación estadística, ANOVA comienza formulando una hipótesis nula y alternativa. Para este ejemplo, las hipótesis son las siguientes:
Hipótesis Nula (H0): No hay diferencia en el precio medio del vino entre los tres países; todos son iguales.
Hipótesis alternativa (H1): El precio medio del vino no es el mismo entre los tres países.
Nota, esta es una pruebaibusnibus, lo que significa que si somos capaces de rechazar la hipótesis nula, nos dirá que existe una diferencia estadísticamente significativa en algún lugar entre estos países, pero no nos dirá dónde está.
Establecer un Nivel de Significancia
El nivel de significancia, o alfa, es la probabilidad de rechazar nuestra hipótesis nula cuando realmente es cierta. En otros términos, es la probabilidad de cometer un error de tipo I.
Normalmente, uno debe sopesar los costos de hacer un error de tipo I vs. un error de Tipo II para determinar el mejor alfa para un experimento, pero para este ejemplo de juguete solo voy a usar el estándar .05 para nuestro valor α.
Calcular una estadística F
La estadística F es simplemente una relación de la varianza entre medias de muestra y la varianza dentro de medias de muestra. Para esta prueba ANOVA, veremos qué tan lejos está el precio promedio del vino de cada país del precio promedio general, y lo dividiremos por cuánta variación en el precio hay dentro de la distribución de muestra de cada país. La fórmula estadística F está debajo, lo que puede parecer complicado hasta que la desglosemos.
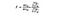
SSB = Suma de cuadrados entre grupos. Esta es la suma de la diferencia al cuadrado entre la media de cada grupo y la media general multiplicada por el número de elementos por grupo. Para este ejemplo, tomamos la media del precio del vino de cada país, la restamos de la media general, cuadramos la diferencia y multiplicamos por 1.000 (el número de puntos de datos por país).
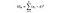
SSE = Suma de cuadrados dentro de los grupos. Esta es la suma de la diferencia cuadrada entre la media del grupo y cada valor en el grupo. Para Francia, tomaríamos el precio medio del vino francés, luego restaríamos y cuadraríamos la diferencia para cada botella de vino francés de los mil puntos de datos en ese grupo.
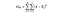
DoFB = Grados de libertad entre grupos, simplemente el número de grupos menos 1. Tenemos tres países diferentes que estamos comparando, por lo que los grados de libertad aquí son 2.
DoFW = Grados de Libertad Dentro de los Grupos, simplemente el número de puntos de datos menos el número de grupos. Tenemos 3.000 puntos de datos y tres países diferentes, así que esto es 2.997 para este ejemplo.
Dividir la suma de cuadrados para un grupo por sus grados de libertad produce los cuadrados medios para ese grupo, y la estadística F es solo una relación de los cuadrados medios entre sobre los cuadrados medios dentro.
A continuación, calculo manualmente estos valores en Python, y termino con una estadística F de ~4.07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
Usando la estadística F, calculamos un valor p
Una vez que tenemos nuestra estadística F, la conectamos a una distribución F para obtener un valor p. Puede encontrar una tabla para estos valores en la parte posterior de cualquier libro de estadísticas o hay calculadoras en línea mucho más fáciles que lo harán por usted. Con nuestros grados de libertad específicos, una estadística F de 4.07 produce un valor p.0172.

Compare el valor p y el nivel de significación para decidir si rechaza o no la hipótesis nula
Nuestro valor p significa que asumiendo que la hipótesis nula (todos los países tienen el mismo precio medio del vino) es verdadera, hay aproximadamente un 1.7% de probabilidad de ver los datos que tenemos por pura probabilidad de muestreo. Al establecer nuestro nivel de significación, o alfa, en el 5% antes de todo esto, dijimos que estaríamos dispuestos a aceptar una probabilidad del 5% de rechazar el nulo cuando sea cierto. Dado que nuestro valor de p está por debajo de nuestro nivel de significación predeterminado, podemos rechazar la hipótesis nula y decir que hay una diferencia estadísticamente significativa en el precio medio del vino entre países.
Recuerde que ANOVA es una pruebaibusnibus, es decir, porque somos capaces de rechazar el null sabemos que existe una diferencia entre los precios medios del vino entre los países, pero no exactamente dónde. Para encontrar dónde radica la diferencia, llevaríamos a cabo pruebas de hipótesis entre dos países a la vez.
ANOVA automática
Al igual que con la mayoría de las cosas de la vida, Python tiene una solución intuitiva para realizar ANOVA con la biblioteca statsmodel. El siguiente código realiza todos los cálculos de este artículo y genera una tabla de resumen completa con una estadística F y un valor p.

Gracias por la lectura, el código completo y los datos se pueden encontrar en mi página de GitHub.