¿Cuál es la mejor unidad de medida para ángulos: revoluciones, grados o radianes?
Revoluciones
Rara vez aprendemos a usar la unidad de medida más simple y natural para ángulos geométricos, la revolución (rev). Otros nombres para esta unidad son círculo completo, giro, giro completo y rotación (rot). Todos estos son buenos nombres y todos significan lo mismo.
1 círculo completo = 1 revolución = 1 giro = 1 putrefacción = 360°
Grados
En la escuela primaria, aprendemos que los ángulos se miden en grados (°).
1 círculo completo= 360°
Radianes
En las clases de trigonometría y cálculo de la escuela secundaria, aprendemos que los matemáticos prefieren los radianes (rad).
1 círculo completo = 2π rad
Nota: Si aún no ha aprendido sobre los radianes en la escuela, puede ignorar los radianes en todo lo que se muestra a continuación.
Comparando revoluciones, Grados y Radianes
Comparemos revoluciones y grados (y radianes).
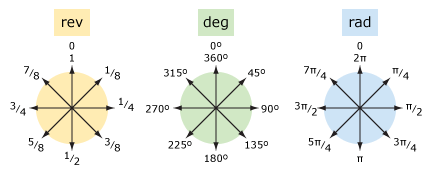
| palabras | rev | deg | rad |
|---|---|---|---|
| no gire | 0 | 0° | 0 |
| cuarto de vuelta | 1/4 | 90° | π/2 |
| media vuelta | 1/2 | 180° | π |
| tres cuartos de vuelta | 3/4 | 270° | 3π/2 |
| la vuelta completa | 1 | 360° | 2π |
| duodécima vez | 1/12 | 30° | π/6 |
| octavo de vuelta | 1/8 | 45° | π/4 |
| sexto turno | 1/6 | 60° | π/3 |
| quinto turno | 1/5 | 72° | 2π/5 |
| tercer turno | 1/3 | 120° | 2π/3 |
| dos vueltas | 2 | 720° | 4π |
| tres vueltas | 3 | 1080° | 6π |
Para convertir de revoluciones grados, se multiplica por 360. Para convertir de grados a revoluciones, divida por 360.
Cuando usa grados, a menudo trabaja con enteros, pero cuando usa revoluciones (o radianes), a menudo trabaja con fracciones (o decimales). Los cálculos manuales a veces son más fáciles cuando se usan revoluciones, pero a veces son más fáciles cuando se usan grados. Es bueno saber las dos cosas.
Las revoluciones son una unidad de medida más racional y natural que los grados. Obtendrás una comprensión más profunda de los ángulos si piensas en revoluciones en lugar de grados. Un ángulo es más fundamentalmente una subdivisión de un círculo que una suma de grados. Por ejemplo, un ángulo recto es fundamentalmente un cuarto de círculo en lugar de una suma de 90 grados.
Dividamos el círculo en n sectores iguales (ver diagrama a continuación). El ángulo de cada sector es 1 / n rev = 360/n° = 2π / n rad. Es más fácil entender esto si piensas en revoluciones en lugar de grados (o radianes).

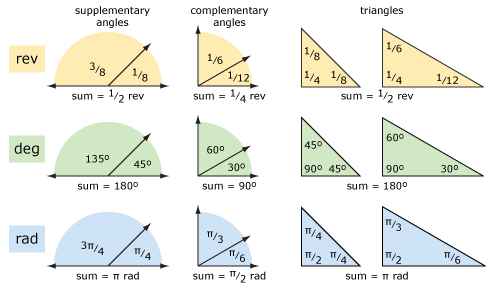
Veamos una geometría básica usando revoluciones y grados (y radianes). El siguiente diagrama muestra ángulos suplementarios, ángulos complementarios y triángulos. Los conceptos son más claros si se piensa en revoluciones en lugar de grados. La aritmética puede ser más fácil usando grados si tiene problemas para sumar y restar fracciones.
Veamos los polígonos (ver el diagrama a continuación). Para un polígono regular con n lados, el ángulo exterior es 1 / n rev = 360/n° = 2π / n rad. Es más fácil entender esto si piensas en revoluciones en lugar de grados (o radianes). El ángulo interior es el complemento del ángulo exterior.

Enseñar Revoluciones, Grados y Radianes
Creo que sería bueno que los maestros introdujeran revoluciones (giros) al mismo tiempo que introducen grados. Esto ayudará a los estudiantes a comprender los ángulos a un nivel más fundamental, menos dependiente del número mágico arbitrario 360. Los maestros ya introducen el concepto general de revoluciones (giros) cuando dicen cosas como «un círculo completo es de 360°», pero pueden hacer que el concepto sea más preciso numéricamente diciendo «un giro completo es de 360°, un medio giro es de 180°, un cuarto de giro es de 90° y un octavo giro es de 45°» o escribiendo «1 revolución = 360°, 1/2 revolución = 180°, 1/4 revolución = 90° y 1/8 revolución = 45°». De vez en cuando, los estudiantes deben practicar haciendo algunos cálculos usando revoluciones (giros) en lugar de grados. Por supuesto, los estudiantes necesitarán pasar la mayor parte de su tiempo aprendiendo a calcular con grados (y más tarde, radianes), porque ese es el estándar.
Ángulos en Trigonometría y Cálculo
Finalmente, echemos un vistazo rápido a las matemáticas más avanzadas: trigonometría y cálculo.
Podemos considerar el uso de revoluciones con funciones trigonométricas (seno, coseno, tangente). Por ejemplo, en lugar de decir cos(60°) = 1/2 o cos(π/3) = 1/2 usando radianes, podríamos decir cos(1/6) = 1/2 usando revoluciones. Pero esto no es práctico porque dependemos de las calculadoras para evaluar las funciones trigonométricas, y las calculadoras típicamente solo tienen modos DEG y RAD, no modo REV.
Cuando pasamos a niveles más profundos de matemáticas, como el cálculo y el análisis matemático, resulta que los radianes son las unidades más racionales y naturales. Por ejemplo, considere esta ecuación fundamental: el límite de pecado (x)/x cuando x se acerca a 0 es exactamente 1. Esta ecuación no sería tan elegante si usáramos cualquier unidad que no sea radianes.