Welches ist die beste Maßeinheit für Winkel – Umdrehungen, Grad oder Bogenmaß?
Umdrehungen
Wir lernen selten, die einfachste und natürlichste Maßeinheit für geometrische Winkel zu verwenden, die Umdrehung (rev). Andere Namen für diese Einheit sind Full Circle, Turn, Full Turn und Rotation (rot). Das sind alles gute Namen und sie bedeuten alle dasselbe.
1 Vollkreis = 1 Umdrehung = 1 Umdrehung = 1 Umdrehung = 360°
Grad
In der Grundschule lernen wir, dass Winkel in Grad (°) gemessen werden.
1 Vollkreis = 360°
Bogenmaß
In der High School Trigonometrie und Kalkül Klassen, lernen wir, dass Mathematiker Bogenmaß (rad) bevorzugen.
1 Vollkreis = 2π rad
Hinweis: Wenn Sie in der Schule noch nichts über das Bogenmaß gelernt haben, können Sie das Bogenmaß in allem Folgenden ignorieren.
Vergleich von Umdrehungen, Grad und Bogenmaß
Vergleichen wir Umdrehungen und Grad (und Bogenmaß).
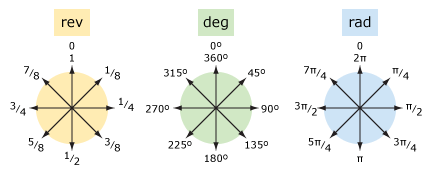
| wörter | rev | Grad | rad |
|---|---|---|---|
| keine Wende | 0 | 0° | 0 |
| vierteldrehung | 1/4 | 90° | π/2 |
| halbe Umdrehung | 1/2 | 180° | π |
| dreiviertel Umdrehung | 3/4 | 270° | 3π/2 |
| volle Umdrehung | 1 | 360° | 2π |
| zwölfte Umdrehung | 1/12 | 30° | π/6 |
| achte Runde | 1/8 | 45° | π/4 |
| sechste Runde | 1/6 | 60° | π/3 |
| fünfte Runde | 1/5 | 72° | 2π/5 |
| dritte Runde | 1/3 | 120° | 2π/3 |
| zwei Umdrehungen | 2 | 720° | 4π |
| drei Umdrehungen | 3 | 1080° | 6π |
Um von Umdrehungen in Grad umzurechnen, multiplizieren Sie mit 360. Um von Grad in Umdrehungen umzurechnen, dividieren Sie durch 360.
Wenn Sie Grad verwenden, arbeiten Sie oft mit ganzen Zahlen, aber wenn Sie Umdrehungen (oder Bogenmaß) verwenden, arbeiten Sie oft mit Brüchen (oder Dezimalzahlen). Handberechnungen sind manchmal einfacher, wenn Sie Umdrehungen verwenden, aber manchmal einfacher, wenn Sie Grad verwenden. Es ist gut, beide Wege zu kennen.
Umdrehungen (Umdrehungen) sind eine rationalere und natürlichere Maßeinheit als Grad. Sie erhalten ein tieferes Verständnis von Winkeln, wenn Sie eher an Umdrehungen als an Grad denken. Ein Winkel ist eher eine Unterteilung eines Kreises als eine Summe von Graden. Zum Beispiel ist ein rechter Winkel eher ein Viertelkreis als eine Summe von 90 Grad.
Teilen wir den Kreis in n gleiche Sektoren (siehe Diagramm unten). Der Winkel jedes Sektors ist 1 / n rev = 360/n° = 2π/n rad. Es ist einfacher, dies zu verstehen, wenn Sie eher an Umdrehungen als an Grad (oder Bogenmaß) denken.

Schauen wir uns einige grundlegende Geometrien mit Umdrehungen und Graden (und Bogenmaß) an. Das folgende Diagramm zeigt Ergänzungswinkel, Komplementärwinkel und Dreiecke. Die Konzepte sind klarer, wenn Sie eher an Umdrehungen als an Grad denken. Die Arithmetik kann mit Grad einfacher sein, wenn Sie Probleme beim Addieren und Subtrahieren von Brüchen haben.
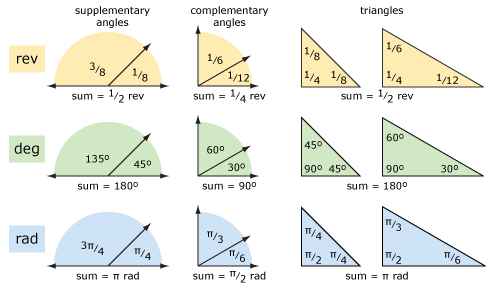
Schauen wir uns Polygone an (siehe Diagramm unten). Für ein reguläres Polygon mit n Seiten beträgt der Außenwinkel 1 / n rev = 360 / n° = 2π / n rad. Es ist einfacher, dies zu verstehen, wenn Sie eher an Umdrehungen als an Grad (oder Bogenmaß) denken. Der Innenwinkel ist die Ergänzung des Außenwinkels.

Lehre Revolutionen, Grad und Bogenmaß
Ich denke, es wäre gut, wenn Lehrer Revolutionen (Wendungen) zur gleichen Zeit einführen würden, in der sie Grade einführen. Dies wird den Schülern helfen, Winkel auf einer grundlegenderen Ebene zu verstehen, die weniger von der willkürlichen magischen Zahl 360 abhängig ist. Lehrer führen das allgemeine Konzept der Umdrehungen bereits ein, wenn sie Dinge wie „ein Vollkreis ist 360 °“ sagen, aber sie können das Konzept numerischer präzisieren, indem sie sagen „eine volle Umdrehung ist 360 °, eine halbe Umdrehung ist 180 °, eine Viertelumdrehung ist 90 ° und eine achte Umdrehung ist 45 °“ oder schreiben „1 Umdrehung = 360 °, 1/2 Umdrehung = 180 °, 1/4 Umdrehung = 90 ° und 1/8 Umdrehung = 45 °“. Die Schüler sollten gelegentlich üben, ein paar Berechnungen mit Umdrehungen (Umdrehungen) anstelle von Grad durchzuführen. Natürlich müssen die Schüler die meiste Zeit damit verbringen, das Berechnen mit Graden (und später mit Bogenmaß) zu lernen, da dies der Standard ist.
Winkel in Trigonometrie und Analysis
Werfen wir zum Schluss einen kurzen Blick auf die fortgeschrittenere Mathematik: Trigonometrie und Analysis.
Wir können in Betracht ziehen, Umdrehungen mit trigonometrischen Funktionen (Sinus, Cosinus, Tangens) zu verwenden. Anstatt beispielsweise cos (60 °) = 1/2 oder cos (π / 3) = 1/2 im Bogenmaß zu sagen, möchten wir möglicherweise cos (1/6) = 1/2 mit Umdrehungen sagen. Dies ist jedoch nicht praktikabel, da wir zur Bewertung der trigonometrischen Funktionen auf Taschenrechner angewiesen sind und Taschenrechner normalerweise nur die Modi DEG und RAD und nicht den REV-Modus haben.
Wenn wir zu tieferen Ebenen der Mathematik wie Kalkül und mathematischer Analyse gehen, stellt sich heraus, dass Bogenmaß die rationalsten und natürlichsten Einheiten sind. Betrachten Sie zum Beispiel diese Grundgleichung: Die Grenze von sin (x) / x, wenn sich x 0 nähert, ist genau 1. Diese Gleichung wäre nicht so elegant, wenn wir eine andere Einheit als das Bogenmaß verwenden würden.