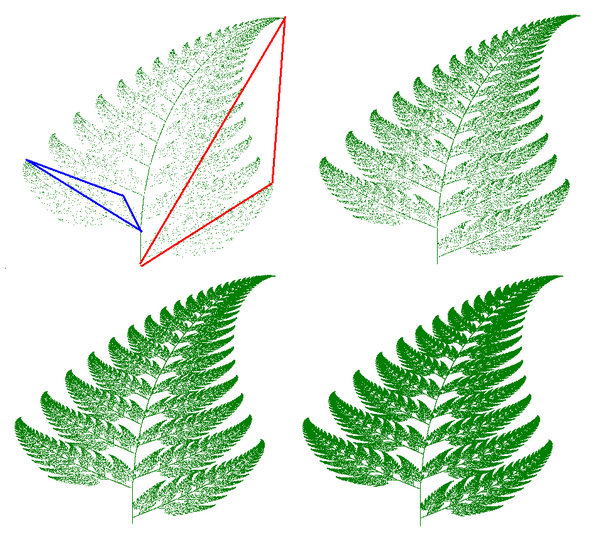
Fractal art repräsentiert die Allianz von Kunst und Mathematik. Diese neuere Kunstform verwendet Computer, um Bilder aus mathematischen Formeln zu erstellen. Fraktale Kunst hat eine oft geometrische Erscheinung, komplizierte Muster und eine Fülle von Details. Aber wie gehen Sie vor, um Bilder aus mathematischen Formeln zu erstellen?
Was bedeutet zunächst „Fraktal“?
In den 1970er Jahren entdeckte der Informatiker Benoit Mandelbrot eines der berühmtesten Fraktalbilder: das Mandelbrot-Set.

Diese Entdeckung wird durch die Entwicklung des Computers ermöglicht, insbesondere dank der Rechenleistung. Es findet auch im wissenschaftlichen Kontext der Entwicklung der Chaostheorie statt, die dynamische Phänomene (Turbulenz, Wirbel in einer Flüssigkeit, Oszillation, Wolkenform usw.) untersucht.).
Ebenso findet sich die fraktale Geometrie in den Formen der Natur mit komplexen Konturen (Schneeflocke, Blatt eines Baumes, Form von Wolken, Wirbeln, Arboreszenz des Blutnetzes, Form von Seeküsten usw.), dass es schwierig war, zu verstehen, und mit den bisherigen mathematischen Werkzeugen zu modellieren.

Merkmale fraktaler Bilder
Die fraktale Dimension
Der Begriff „Fraktal“ bezieht sich auf die Idee einer nicht ganzen, gebrochenen Dimension. Bis in die 1960er Jahre untersuchte die Mathematik zerlegbare Objekte mit ganzzahligen Dimensionen:
ein Punkt: Dimension 0
eine Linie: Dimension 1
ein Plan: Dimension 2
ein Volumen: Dimension 3
Aber stellen Sie sich ein Blatt Papier vor. Es stellt eine Ebene dar und hat daher eine Dimension gleich 2. Wenn wir dieses Blatt zerknittern, nimmt es jetzt ein Volumen ein (Dimension 3), ist aber kein Volumen, da wir das zerknitterte Blatt nicht mit einem Material „füllen“ können, wie man es in einem Behälter tun würde. Das Maß des zerknitterten Blattes liegt daher beispielsweise zwischen 2 und 3:2,568. Eine fraktale Dimension! Fraktale Objekte haben also komplexe, unregelmäßige Formen, deren Konturen in sich gefaltet und gefaltet sind.
Selbstähnlichkeit
Trotz seiner Komplexität weist ein fraktales Objekt ähnliche Details auf. Das Zoomen in ein Fraktal zeigt dasselbe Gesamtmuster, das sich in verschiedenen Maßstäben und bis ins Unendliche wiederholt. Ein Teil ist also dem Ganzen ähnlich. Diese Eigenschaft wird Skaleninvarianz genannt.

Typologie
Fraktale nach Wiederholung
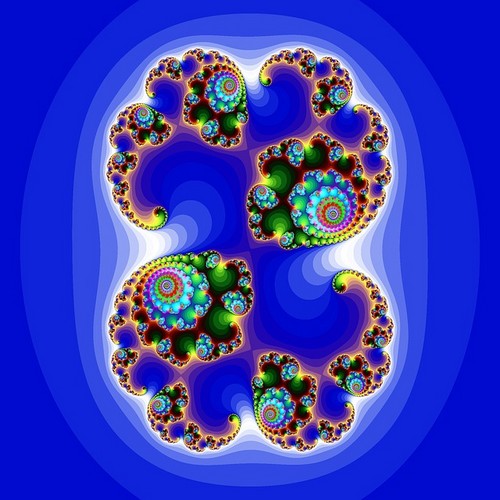

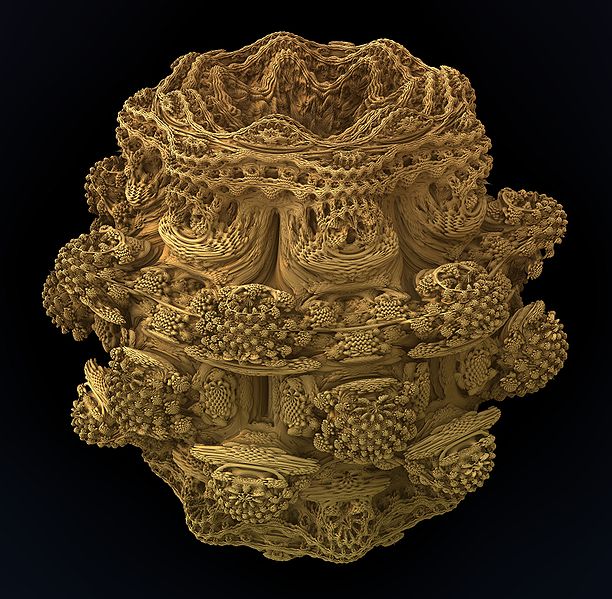
IFS, iterierte Funktionssysteme



Erzeugung von Fraktalbildern, „Einfachheit erzeugt Komplexität“
Die Konstruktion von Fraktalbildern basiert auf der Verwendung eines Algorithmus, der in einer Schleife ausgeführt wird. Es ist ein iterativer Prozess, der eine Reihe einfacher Operationen wiederholt.
Fraktale durch Wiederholung
Für jeden Punkt im Raum werden die Koordinaten des Punktes in eine Gleichung übergeben. Das Ergebnis wird dann in dieselbe Gleichung zurückgeführt. Die Operation wird mehrmals hintereinander ausgeführt (Iterationen). Dann testen wir das Ergebnis. Wenn das Ergebnis gegen unendlich tendiert, liegt der Ausgangspunkt nicht im Ganzen : Es ist weiß gefärbt. Wenn das Ergebnis stabil oder periodisch bleibt, liegt der Ausgangspunkt im Ganzen : Es ist schwarz gefärbt. Für Punkte an der Grenze ist es schwieriger zu bestimmen, ob sie sich in der Menge oder außerhalb befinden. Es ist dann notwendig, weitere Iterationen durchzuführen. Abhängig von der Anzahl der Iterationen, die erforderlich sind, um den Punkt zu bestimmen, wird er in verschiedenen Farbtönen gefärbt. Die Punkte dieser Grenze geben dem Fraktal sein kompliziertes und verworrenes Aussehen.
Um die Mandelbrot-Menge zu zeichnen, verwenden wir komplexe Zahlen, die jeweils ein Pixel in der Ebene darstellen. Wir führen die folgende Gleichung für jeden Punkt aus: Zn + 1 = Zn2 + C, mit Z0 = 0.
IFS, iterated functions systems
Die Bildkonstruktion erfolgt hier durch Kopieren selbst. Aber mit jeder Kopie erfährt das kopierte Bild eine geometrische Transformation (eine lineare Transformation, die in der Mathematik durch eine lineare Funktion dargestellt wird). Diese Transformationen können Rotationen, Abflachungen, Scheren sein … Die Kopien werden auch zusammengezogen, bevor sie wieder auf dem Originalbild platziert werden. Der Vorgang wird wiederholt, bis ein Bild entsteht.
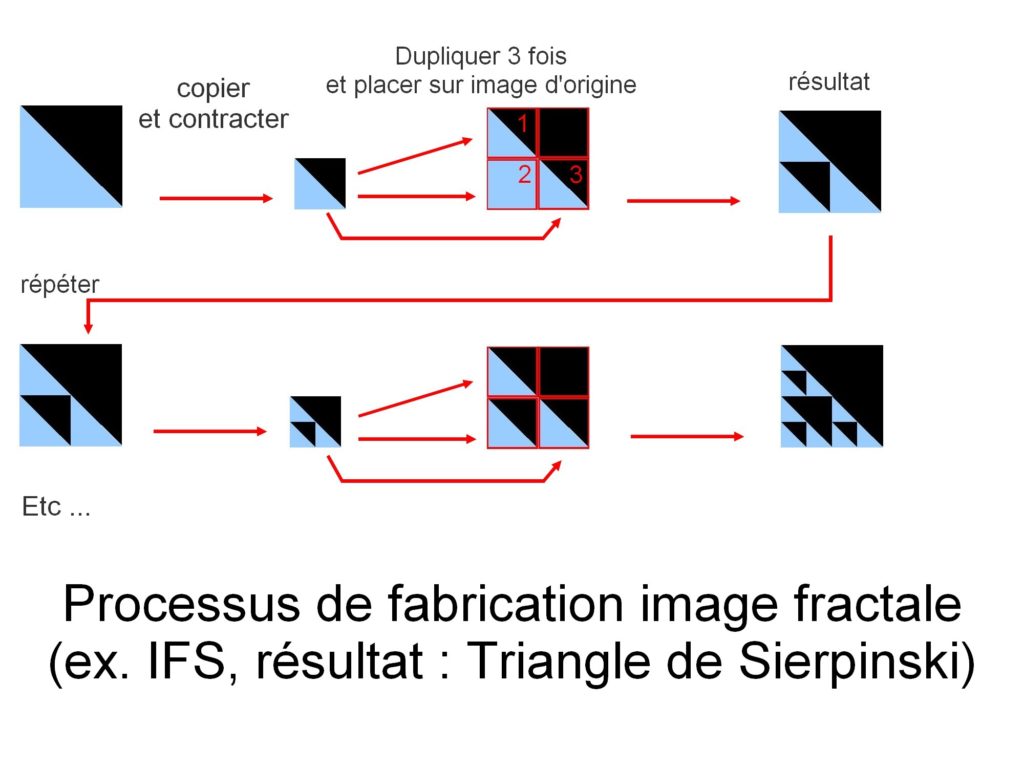
Dieses Beispiel ergibt das Bild des Sierpinski-Dreiecks.
Ein weiteres Beispiel ist die Erzeugung der Koch-Schneeflocke.

IFS kann leicht Bilder erzeugen, die an natürliche Objekte wie Bäume, Farne usw. erinnern.