ANOVA am Beispiel erklärt

Hintergrund

Die Varianzanalyse, typischerweise als ANOVA bezeichnet, wird in einführenden Statistikkursen oft beschönigt. Mit der heutigen Technologie ist es einfach, den Computer alle Berechnungen durchführen zu lassen und nur den p-Wert am Ende einer beschäftigt aussehenden Tabelle wie der obigen zu betrachten. In diesem Artikel werde ich durchgehen, was diese Zahlen sind und was ANOVA tatsächlich tut.

Die Hauptidee hinter ANOVA ist es, zu testen, ob es einen statistisch signifikanten Unterschied in den gemessenen Mitteln zwischen Untergruppen einer Probe gibt. Das Konzept stammt aus der Zeit um 1920 mit einem britischen Statistiker namens Ronald Fisher, der riesige Datenmengen über Ernteerträge analysierte. Fisher verwendete ANOVA, um zu beweisen, dass es einen signifikanten Unterschied im Durchschnittsgewicht von Kartoffeln gab, wenn verschiedene Düngemittel verwendet wurden.

Um eine ANOVA in der Gegenwart zu demonstrieren, werde ich eher die Preise für Wein als die Gewichte von Kartoffeln betrachten. Die Daten für dieses Beispiel stammen aus Kaggles Wine Review-Datensatz, der Tausende von Bewertungen zu Weinflaschen von WineEnthusiast enthält. Ich habe es auf eine Teilmenge von 3.000 Bewertungen für Weine aus den USA, Italien und Frankreich (1.000 pro Land) gefiltert und werde ANOVA verwenden, um zu testen, ob es einen statistisch signifikanten Unterschied im Durchschnittspreis zwischen den Herkunftsländern gibt.

Eine schnelle Darstellung der Preisverteilung nach Ländern zeigt drei ziemlich ähnliche Verteilungen, wobei die meisten Preise bei etwa 25 USD pro Flasche liegen.

Wenn wir den Mittelwert jedes Landes nehmen, sehen wir, dass Frankreich im Durchschnitt den teuersten Wein hat, gefolgt von Italien und schließlich den USA. Aber die Frage ist, ist dies ein echter Preisunterschied zwischen den Ländern oder könnte dies nur auf Stichprobenvariationen zurückzuführen sein? Hier kommt ANOVA ins Spiel.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

Die vier Schritte zur ANOVA sind:

1. Formulieren Sie eine Hypothese
2. Setzen Sie ein Signifikanzniveau
3. Berechnen Sie eine F-Statistik
4. Verwenden Sie die F-Statistik, um einen p-Wert
5 abzuleiten. Vergleichen Sie den p-Wert und das Signifikanzniveau, um zu entscheiden, ob die Nullhypothese abgelehnt werden soll oder nicht

Formulieren Sie eine Hypothese

Wie bei fast allen statistischen Signifikanztests beginnt ANOVA mit der Formulierung einer Null- und Alternativhypothese. Für dieses Beispiel lauten die Hypothesen wie folgt:

Nullhypothese (H0): Es gibt keinen Unterschied im Durchschnittspreis für Wein zwischen den drei Ländern; sie sind alle gleich.
Alternativhypothese (H1): Der durchschnittliche Weinpreis ist zwischen den drei Ländern nicht gleich.

Beachten Sie, dass dies ein Omnibus-Test ist, dh wenn wir die Nullhypothese ablehnen können, wird es uns sagen, dass irgendwo zwischen diesen Ländern ein statistisch signifikanter Unterschied besteht, aber es wird uns nicht sagen, wo es ist.

Legen Sie ein Signifikanzniveau fest

Das Signifikanzniveau oder Alpha ist die Wahrscheinlichkeit, unsere Nullhypothese abzulehnen, wenn sie tatsächlich zutrifft. Mit anderen Worten, es ist die Wahrscheinlichkeit, einen Typ-I-Fehler zu machen.

Normalerweise sollte man die Kosten für einen Fehler vom Typ I gegen einen Fehler vom Typ II abwägen, um das beste Alpha für ein Experiment zu bestimmen, aber für dieses Spielzeugbeispiel werde ich nur den Standard verwenden .05 für unseren α-Wert.

Berechnen Sie eine F-Statistik

Die F-Statistik ist einfach ein Verhältnis der Varianz zwischen den Stichprobenmitteln zur Varianz innerhalb der Stichprobenmittel. Für diesen ANOVA-Test untersuchen wir, wie weit der durchschnittliche Weinpreis jedes Landes vom Gesamtdurchschnittspreis entfernt ist, und dividieren diesen durch die Preisunterschiede innerhalb der Stichprobenverteilung jedes Landes. Die F-Statistik Formel ist unten, die kompliziert aussehen kann, bis wir es brechen.

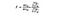
SSB = Summe der Quadrate zwischen Gruppen. Dies ist die Summe der quadratischen Differenz zwischen dem Mittelwert jeder Gruppe und dem Gesamtmittelwert mal der Anzahl der Elemente pro Gruppe. Für dieses Beispiel nehmen wir den Mittelwert des Weinpreises jedes Landes, subtrahieren ihn vom Gesamtmittelwert, quadrieren die Differenz und multiplizieren sie mit 1.000 (der Anzahl der Datenpunkte pro Land).

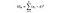
SSW = Summe der Quadrate innerhalb von Gruppen. Dies ist die Summe der quadratischen Differenz zwischen dem Gruppenmittelwert und jedem Wert in der Gruppe. Für Frankreich würden wir den mittleren Preis für französischen Wein nehmen, dann die Differenz für jede Flasche französischen Weins von den tausend Datenpunkten in dieser Gruppe subtrahieren und quadrieren.

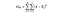
DoFB = Freiheitsgrade zwischen Gruppen, einfach die Anzahl der Gruppen minus 1. Wir haben drei verschiedene Länder, die wir vergleichen, also sind die Freiheitsgrade hier 2.
DoFW = Freiheitsgrade innerhalb von Gruppen, einfach die Anzahl der Datenpunkte minus der Anzahl der Gruppen. Wir haben 3.000 Datenpunkte und drei verschiedene Länder, also sind dies 2.997 für dieses Beispiel.

Wenn man die Summe der Quadrate für eine Gruppe durch ihre Freiheitsgrade dividiert, erhält man die mittleren Quadrate für diese Gruppe, und die F-Statistik ist nur ein Verhältnis der mittleren Quadrate zwischen über den mittleren Quadraten innerhalb.

Unten berechne ich diese Werte manuell in Python und erhalte eine F-Statistik von ~4.07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

Berechnen Sie mit der F-Statistik einen p-Wert

Sobald wir unsere F-Statistik haben, schließen wir sie an eine F-Verteilung an, um einen p-Wert zu erhalten. Sie können eine Tabelle für diese Werte auf der Rückseite jedes Statistikbuchs finden, oder es gibt viel einfachere Online-Rechner, die dies für Sie tun. Mit unseren spezifischen Freiheitsgraden ergibt eine F-Statistik von 4,07 einen p-Wert.0172.

Vergleichen Sie den p-Wert und das Signifikanzniveau, um zu entscheiden, ob die Nullhypothese abgelehnt werden soll oder nicht

Unser p-Wert bedeutet, dass unter der Annahme, dass die Nullhypothese (alle Länder haben den gleichen mittleren Weinpreis) zutrifft, ungefähr eine 1 vorliegt.7% Chance, die Daten, die wir haben, durch reine Stichprobenchance zu sehen. Indem wir unser Signifikanzniveau oder Alpha vor all dem auf 5% festlegten, sagten wir, dass wir bereit wären, eine 5% ige Chance zu akzeptieren, die Null abzulehnen, wenn sie wahr ist. Da unser p-Wert unter unserem vorher festgelegten Signifikanzniveau liegt, können wir die Nullhypothese ablehnen und sagen, dass es einen statistisch signifikanten Unterschied im mittleren Weinpreis zwischen den Ländern gibt.

Denken Sie daran, dass ANOVA ein Omnibus-Test ist, dh weil wir die Null ablehnen können, wissen wir, dass ein Unterschied zwischen den durchschnittlichen Weinpreisen zwischen den Ländern besteht, aber nicht genau wo. Um herauszufinden, wo der Unterschied liegt, würden wir dann Hypothesentests zwischen jeweils zwei Ländern durchführen.

Automatische ANOVA

Wie bei den meisten Dingen im Leben bietet Python eine intuitive Lösung für die Durchführung von ANOVA mit der Statsmodel-Bibliothek. Der folgende Code führt alle Berechnungen in diesem Artikel durch und gibt eine Übersichtstabelle mit einer F-Statistik und einem p-Wert aus.

Danke fürs Lesen, vollständiger Code und Daten finden Sie auf meiner GitHub-Seite.