vilken är den bästa måttenheten för vinklar — varv, grader eller radianer?
varv
vi lär oss sällan att använda den enklaste, mest naturliga måttenheten för geometriska vinklar, revolutionen (rev). Andra namn för denna enhet är full cirkel, sväng, full sväng och rotation (rot). Dessa är alla bra namn och de betyder alla samma sak.
1 full cirkel = 1 varv = 1 varv = 1 rot = 360°
grader
i grundskolan lär vi oss att vinklarna mäts i grader (Brasilien).
1 hela cirkeln = 360°
radianer
i gymnasiet trigonometri och kalkylklasser lär vi oss att matematiker föredrar radianer (rad).
1 Full circle = 2 occubic rad
Obs: Om du ännu inte har lärt dig om radianer i skolan kan du ignorera radianerna i allt nedan.
jämföra varv, grader och radianer
Låt oss jämföra varv och grader (och radianer).
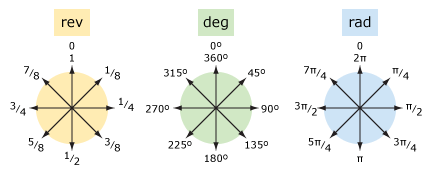
| ord | varv | ° | rad |
|---|---|---|---|
| ingen tur | 0 | 0° | 0 |
| kvarts varv | 1/4 | 90° | π/2 |
| halvt varv | 1/2 | 180° | π |
| tre-kvarts varv | 3/4 | 270° | 3π/2 |
| full turn | 1 | 360° | 2π |
| tolfte stäng | 1/12 | 30° | π/6 |
| åttonde stäng | 1/8 | 45° | π/4 |
| sjätte stäng | 1/6 | 60° | π/3 |
| femte stäng | 1/5 | 72° | 2π/5 |
| tredje tur | 1/3 | 120° | 2π/3 |
| två varv | 2 | 720° | 4π |
| tre varv | 3 | 1080° | 6π |
för Att konvertera från varv till grader, multiplicera med 360. För att konvertera från grader till varv, dela med 360.
när du använder grader arbetar du ofta med heltal, men när du använder varv (eller radianer) arbetar du ofta med bråk (eller decimaler). Handberäkningar är ibland enklare när du använder varv men ibland lättare när du använder grader. Det är bra att veta båda sätten.
varv (varv) är en mer rationell och naturlig måttenhet än grader. Du får en djupare förståelse för vinklar om du tänker på revolutioner snarare än grader. En vinkel är mer grundläggande en indelning av en cirkel snarare än en summa av grader. Till exempel är en rätt vinkel mer fundamentalt en fjärdedel av en cirkel snarare än en summa av 90 grader.
låt oss dela cirkeln i n lika sektorer (se diagram nedan). Vinkeln för varje sektor är 1/n rev = 360/n 0BG = 2 2BG / n rad. Det är lättare att förstå detta om du tänker på revolutioner snarare än grader (eller radianer).

Låt oss titta på några grundläggande geometri med hjälp av varv och grader (och radianer). Diagrammet nedan visar kompletterande vinklar, kompletterande vinklar och trianglar. Begreppen är tydligare om du tänker på revolutioner snarare än grader. Aritmetiken kan vara lättare att använda grader om du har problem med att lägga till och subtrahera fraktioner.
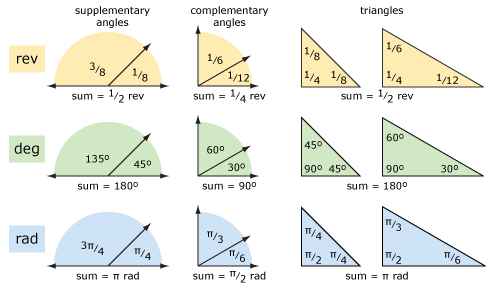
Låt oss titta på polygoner (se diagram nedan). För en vanlig polygon med n-sidor är den yttre vinkeln 1/n rev = 360/n 0CB = 2 2CB / n rad. Det är lättare att förstå detta om du tänker på revolutioner snarare än grader (eller radianer). Den inre vinkeln är tillägget av den yttre vinkeln.

undervisning revolutioner, grader och radianer
jag tror att det skulle vara bra om lärare skulle införa revolutioner (svängar) samtidigt som de introducerar grader. Detta kommer att hjälpa eleverna att förstå vinklar på en mer grundläggande nivå, mindre beroende av det godtyckliga magiska numret 360. Lärare redan inför de allmänna begreppet varvtal (varv) när de säger saker som ”en full cirkel är 360°”, men de kan göra begreppet mer numeriskt exakt genom att säga ”ett helt varv är 360°, ett halvt varv är 180°, ett kvarts varv är 90°, och en åttonde tur är 45°” eller genom att skriva ”1 varv = 360°, 1/2 rev = 180°, 1/4 varv = 90°, och 1/8 rev = 45°”. Eleverna bör ibland öva på att göra några beräkningar med hjälp av varv (varv) snarare än grader. Naturligtvis kommer eleverna att behöva spendera större delen av sin tid på att lära sig att beräkna med grader (och senare radianer), för det är standarden.
vinklar i trigonometri och kalkyl
slutligen, låt oss ta en snabb titt på mer avancerad matematik: trigonometri och kalkyl.
vi kan överväga att använda varv med trigonometriska funktioner (sinus, cosinus, tangent). Till exempel, i stället för att säga cos(60 2BG) = 1/2 eller cos(3BG) = 1/2 med hjälp av radianer, kanske vi vill säga cos(1/6) = 1/2 med hjälp av varv. Men det här är inte praktiskt eftersom vi är beroende av räknare för att utvärdera de trigonometriska funktionerna, och räknare har vanligtvis bara DEG-och RAD-lägen, inte REV-läge.
när vi går till djupare nivåer av matematik, såsom kalkyl och matematisk analys, visar det sig att radianer är de mest rationella och naturliga enheterna. Tänk till exempel på denna grundläggande ekvation: gränsen för synd(x)/x när x närmar sig 0 är exakt 1. Denna ekvation skulle inte vara så elegant om vi använde någon annan enhet än radianer.