Fraktalkonst representerar alliansen mellan konst och matematik. Denna senaste konstform använder datorer för att göra bilder från matematiska formler. Fraktalkonst har ett ofta geometriskt utseende, invecklade mönster och en mängd detaljer. Men hur gör du för att skapa bilder från matematiska formler ?
först och främst, vad betyder ”fraktal”?
på 1970-talet upptäckte datavetenskaparen Benoit Mandelbrot en av de mest kända fraktalbilderna: Mandelbrot-uppsättningen.

denna upptäckt möjliggörs genom utveckling av dator, särskilt tack vare datorkraften. Det sker också i det vetenskapliga sammanhanget av utvecklingen av kaosteorin som studerar dynamiska fenomen (turbulens, virvlar i en vätska, svängning, molnform etc.).
på samma sätt finns fraktalgeometri i naturens former med komplexa konturer (snöflinga, löv av ett träd, form av moln, virvlar, arborescens av blodnätet, form av maritima kuster etc.) att det var svårt att förstå och att modellera med de tidigare matematiska verktygen.

egenskaper för fraktala bilder
fraktaldimensionen
termen ”fraktal” avser tanken på en icke-hel, fraktionerad dimension. Fram till 1960-talet studerade matematik nedbrytbara objekt med heltalsdimensioner:
en punkt: dimension 0
en rad: dimension 1
en plan: dimension 2
en volym: dimension 3
men föreställ dig ett pappersark. Det representerar ett plan, har därför en dimension som är lika med 2. Om vi skrynklar detta ARK upptar det nu en volym (dimension 3), men är inte en volym eftersom vi inte kan ”fylla” det skrynkliga arket med ett material som man skulle fylla en behållare. Dimensionen på det skrynkliga arket är därför mellan 2 och 3 : 2.568 till exempel. En fraktal dimension ! Fraktala föremål har således komplexa, oregelbundna former, med konturer vikta och vikta in på sig själva.
Självlikhet
trots dess komplexitet uppvisar ett fraktalobjekt liknande detaljer. Zoomning inuti en fraktal visar samma övergripande mönster som upprepas i olika skalor och in i oändligheten. En del liknar därför helheten. Den här egenskapen kallas scale invariance.

typologi
fraktaler genom återfall

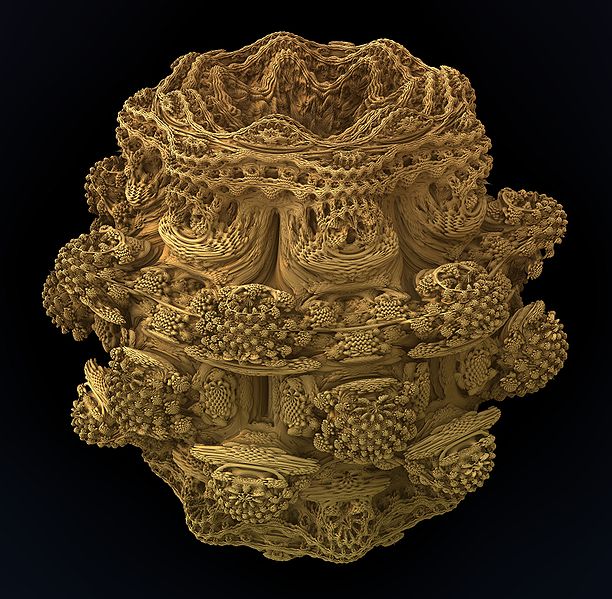
IFS, itererade funktionssystem



generering av fraktala bilder, ”enkelhet raser komplexitet”
konstruktionen av fraktala bilder är baserad på användningen av algoritmen exekveras i en slinga. Det är en iterativ process som upprepar en serie enkla operationer.
fraktaler genom återfall
för varje punkt i rymden passeras koordinaterna för punkten till en ekvation. Resultatet matas sedan tillbaka till samma ekvation. Operationen utförs flera gånger i rad (iterationer). Sedan testar vi resultatet. Om resultatet tenderar till oändlighet, är utgångspunkten inte i det hela : det är färgat vitt. Om resultatet förblir stabilt eller periodiskt, är utgångspunkten i det hela : det är färgat svart. För punkter på gränsen är det svårare att avgöra om de är i uppsättningen eller utanför. Det är då nödvändigt att utföra fler iterationer. Beroende på antalet iterationer som krävs för att bestämma punkten är den färgad i olika nyanser. Punkterna i denna gräns ger fraktalen sitt komplicerade och trassliga utseende.
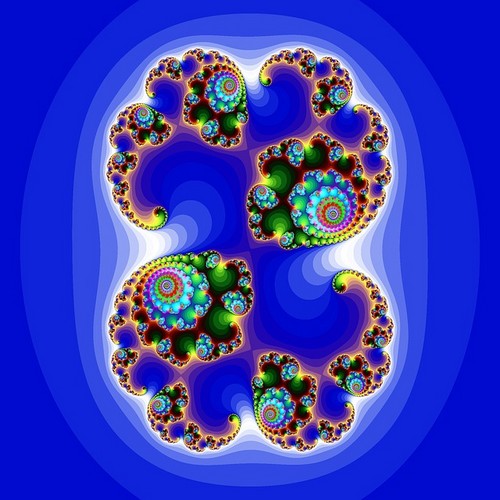
för att rita Mandelbrot-uppsättningen använder vi komplexa tal som var och en representerar en pixel på planet. Vi utför följande ekvation för varje punkt : Zn + 1 = Zn2 + C, med Z0 = 0.
IFS, iterated functions systems
Bildkonstruktion görs här genom att kopiera sig själv. Men med varje kopia genomgår den kopierade bilden en geometrisk transformation (en linjär transformation representerad i matematik med en linjär funktion). Dessa omvandlingar kan vara rotationer, plattning, klippning … kopiorna kontraheras också innan de placeras tillbaka på originalbilden. Processen upprepas tills en bild bildas.
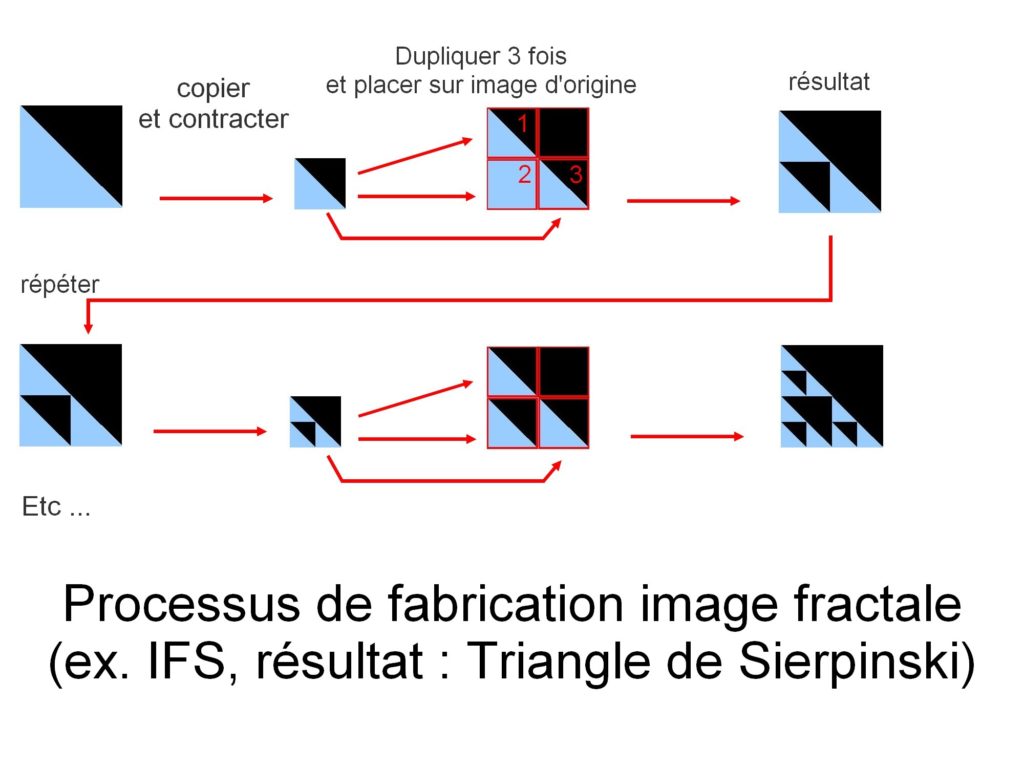
detta exempel resulterar i bilden av Sierpinski-triangeln.
ett annat exempel är generationen av Koch snowflake.

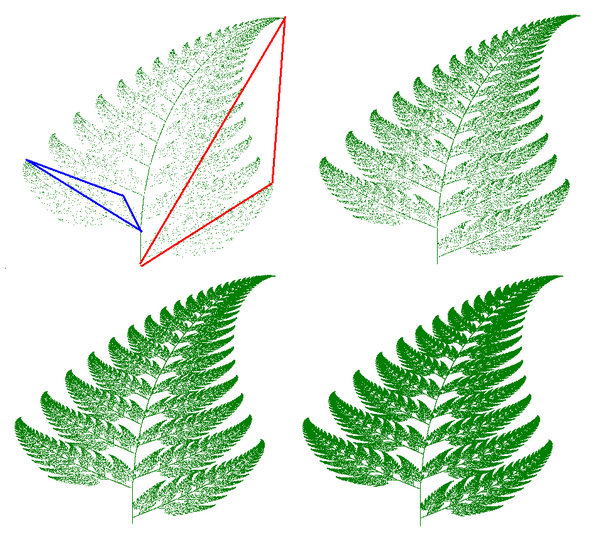
IFS kan enkelt producera bilder som påminner om naturliga föremål, som träd, ormbunkar etc.