ANOVA förklaras med exempel

Bakgrund

variansanalys, vanligtvis kallad ANOVA, är något som ofta glansas över i inledande statistikklasser. Med dagens teknik är det enkelt att låta datorn göra alla beräkningar och bara titta på p-värdet i slutet av ett upptagen bord som det ovan. I den här artikeln ska jag gå igenom vad dessa siffror är och vad ANOVA faktiskt gör.

huvudtanken bakom ANOVA är att testa om det finns en statistiskt signifikant skillnad i ett uppmätt medel mellan undergrupper av ett prov. Konceptet går tillbaka till omkring 1920 med en brittisk statistiker som heter Ronald Fisher, som analyserade enorma mängder data om avkastning. Fisher använde ANOVA för att bevisa att det var en signifikant skillnad i potatisens genomsnittliga vikt när olika gödningsmedel användes.

för att demonstrera ANOVA i dag kommer jag att titta på priserna på vin snarare än potatisvikterna. Uppgifterna för detta exempel är från Kaggles Wine Review dataset, som innehåller tusentals recensioner på flaskor vin från WineEnthusiast. Jag har filtrerat ner det till en delmängd av 3000 recensioner för viner från USA, Italien och Frankrike (1000 per land) och kommer att använda ANOVA för att testa om det finns en statistiskt signifikant skillnad i genomsnittspriset mellan ursprungsländerna.

en snabb plot av prisfördelningen per land visar tre ganska liknande distributioner, med majoriteten av priserna runt $25 per flaska.

med medelvärdet av varje land ser vi att Frankrike har det dyraste vinet i genomsnitt, följt av Italien och slutligen USA. Men frågan är, är detta en verklig prisskillnad mellan länder eller kan det bara bero på provvariation? Det är här ANOVA spelar in.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

de fyra stegen till ANOVA är:

1. Formulera en hypotes
2. Ställ in en signifikansnivå
3. Beräkna en f-statistik
4. Använd F-statistiken för att härleda ett p-värde
5. Jämför p-värde och signifikansnivå för att bestämma huruvida nollhypotesen ska avvisas

formulera en hypoteser

som med nästan alla statistiska signifikanstester börjar ANOVA med att formulera en null-och alternativ hypotes. För detta exempel är hypoteserna följande:

nollhypotes (H0): Det finns ingen skillnad i genomsnittspriset på vin mellan de tre länderna, de är alla desamma.
alternativ hypotes (H1): det genomsnittliga priset på vin är inte detsamma mellan de tre länderna.

Obs, Detta är ett omnibustest, vilket betyder att om vi kan avvisa nollhypotesen kommer det att berätta för oss att en statistiskt signifikant skillnad finns någonstans mellan dessa länder, men det kommer inte att berätta var det är.

Ställ in en signifikansnivå

signifikansnivån, eller alfa, är sannolikheten att avvisa vår nollhypotes när den faktiskt gäller. I andra termer är det sannolikheten att göra ett typ i-fel.

vanligtvis bör man väga kostnaderna för att göra ett typ I vs ett typ II-fel för att bestämma den bästa alfa för ett experiment, men för detta leksaksexempel ska jag bara använda standarden .05 för vårt värde i enlighet med vårt värde.

Beräkna en F-statistik

F-statistiken är helt enkelt ett förhållande mellan variansen mellan provmedel och variansen inom provmedel. För detta ANOVA-test tittar vi på hur långt varje lands genomsnittliga vinpris är från det totala genomsnittspriset och dividerar det med hur mycket variation i pris Det finns inom varje lands provfördelning. F-statistikformeln är nedan, vilket kan se komplicerat ut tills vi bryter ner det.

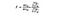
SSB = summan av kvadrater mellan grupper. Detta är summan av den kvadrerade skillnaden mellan varje grupps medelvärde och det totala medelvärdet gånger antalet element per grupp. I det här exemplet tar vi medelvärdet av varje lands vinpris, subtraherar det från det totala medelvärdet, kvadrerar skillnaden och multiplicerar med 1000 (antalet datapunkter per land).

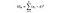
SSW = summan av kvadrater inom grupper. Detta är summan av den kvadrerade skillnaden mellan gruppmedelvärdet och varje värde i gruppen. För Frankrike skulle vi ta medelpriset på franskt vin, sedan subtrahera och kvadrera skillnaden för varje flaska franskt vin av de tusen datapunkterna i den gruppen.

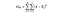
DoFB = frihetsgrader mellan grupper, helt enkelt antalet grupper minus 1. Vi har tre olika länder vi jämför, så frihetsgraderna här är 2.
DoFW = frihetsgrader inom grupper, helt enkelt antalet datapunkter minus antalet grupper. Vi har 3 000 datapunkter och tre olika länder, så det här är 2 997 för det här exemplet.

att dividera summan av kvadrater för en grupp med dess frihetsgrader ger medelkvadraterna för den gruppen, och f-statistiken är bara ett förhållande mellan medelkvadraterna mellan över medelkvadraterna inom.

nedan beräknar jag manuellt dessa värden i Python och slutar med en F-statistik på ~4.07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

med hjälp av F-statistiken beräknar vi ett p-värde

när vi har vår F-statistik kopplar vi den till en F-distribution för att få ett p-värde. Du kan hitta en tabell för dessa värden på baksidan av någon statistik bok eller det finns mycket enklare online räknare som kommer att göra detta åt dig. Med våra specifika frihetsgrader ger en F-statistik på 4,07 ett p-värde .0172.

jämför p-värdet och signifikansnivån för att bestämma huruvida nollhypotesen ska avvisas

vårt p-värde betyder att antagandet av nollhypotesen (alla länder har samma medelpris på vin) är sant, det finns ungefär en 1.7% chans att se de data vi har genom ren samplingschans. Genom att ställa in vår signifikansnivå, eller alfa, på 5% före allt detta, sa vi att vi skulle vara villiga att acceptera en 5% chans att avvisa null när det är sant. Eftersom vårt p-värde ligger under vår förutbestämda signifikansnivå kan vi avvisa nollhypotesen och säga att det finns en statistiskt signifikant skillnad i medelpriset på vin mellan länder.

kom ihåg att ANOVA är ett omnibustest, vilket betyder att vi kan avvisa nollan vi vet att det finns en skillnad mellan de genomsnittliga vinpriserna mellan länder, men inte exakt var. För att hitta var skillnaden ligger skulle vi sedan genomföra hypotesprov mellan två länder i taget.

Automatisk ANOVA

precis som med det mesta i livet har Python en intuitiv lösning för att dirigera ANOVA med statsmodel-biblioteket. Nedanstående kod gör alla beräkningar i den här artikeln och matar ut en sammanfattande tabell komplett med en F-statistik och p-värde.

Tack för att du läste, full kod och data finns på min GitHub-sida.