care este cea mai bună unitate de măsură pentru unghiuri-revoluții, grade sau radiani?
revoluții
rareori învățăm să folosim cea mai simplă și mai naturală unitate de măsură pentru unghiurile geometrice, Revoluția (rev). Alte nume pentru această unitate sunt cerc complet, viraj, viraj complet și rotație (rot). Toate acestea sunt nume bune și toate înseamnă același lucru.
1 cerc complet = 1 rev = 1 turn = 1 rot = 360°
gradele
în școala primară, aflăm că unghiurile sunt măsurate în grade (XV).
1 cerc complet = 360°
radiani
în clasele de trigonometrie și calcul din liceu, aflăm că matematicienii preferă radianii (rad).
1 cerc complet = 2 Rad
Notă: Dacă nu ați învățat încă despre radiani în școală, puteți ignora radianii în tot ceea ce este mai jos.
comparând revoluțiile, gradele și Radianii
să comparăm revoluțiile și gradele (și radianii).
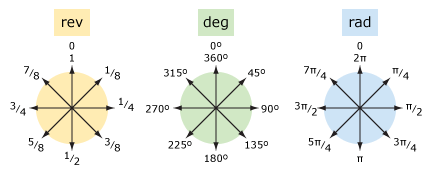
| cuvinte | rev | deg | rad |
|---|---|---|---|
| nu transforma | 0 | 0° | 0 |
| sfert de tura | 1/4 | 90° | π/2 |
| jumătate de tură | 1/2 | 180° | π |
| trei-sfert de tură | 3/4 | 270° | 3π/2 |
| rotație completă | 1 | 360° | 2π |
| douăsprezecea transforma | 1/12 | 30° | π/6 |
| a opta transforma | 1/8 | 45° | π/4 |
| al șaselea turn | 1/6 | 60° | π/3 |
| al cincilea turn | 1/5 | 72° | 2π/5 |
| al treilea turn | 1/3 | 120° | 2π/3 |
| două ture | 2 | 720° | 4n |
| trei ture | 3 | 1080° | 6π |
pentru a converti de La revoluțiile în grade, înmulțiți cu 360. Pentru a converti de la grade la revoluții, împărțiți la 360.
când utilizați grade lucrați adesea cu numere întregi, dar când utilizați revoluții (sau radiani) lucrați adesea cu fracții (sau zecimale). Calculele de mână sunt uneori mai ușor atunci când utilizați revoluții, dar, uneori, mai ușor atunci când utilizați grade. E bine să știi în ambele sensuri.
revoluțiile (virajele) sunt o unitate de măsură mai rațională și mai naturală decât gradele. Veți obține o înțelegere mai profundă a unghiurilor dacă vă gândiți mai degrabă la revoluții decât la grade. Un unghi este mai fundamental o subdiviziune a unui cerc decât o sumă de grade. De exemplu, un unghi drept este mai fundamental un sfert de cerc decât o sumă de 90 de grade.
Să împărțim cercul în n sectoare egale (vezi diagrama de mai jos). Unghiul fiecărui sector este de 1 / n rev = 360 / n 0tct = 2 xtct / n rad. Este mai ușor să înțelegeți acest lucru dacă vă gândiți mai degrabă la revoluții decât la grade (sau radiani).

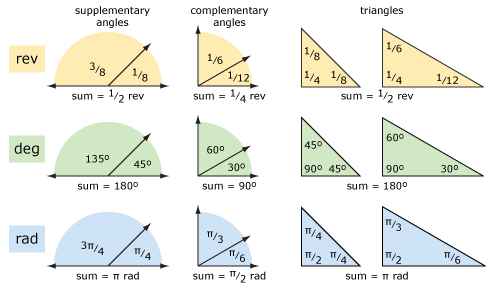
să ne uităm la o geometrie de bază folosind revoluții și grade (și radiani). Diagrama de mai jos prezintă unghiuri suplimentare, unghiuri complementare și triunghiuri. Conceptele sunt mai clare dacă vă gândiți mai degrabă la revoluții decât la grade. Aritmetica poate fi mai ușoară folosind grade dacă aveți probleme la adăugarea și scăderea fracțiilor.
să ne uităm la poligoane (vezi diagrama de mai jos). Pentru un poligon regulat cu n laturi, unghiul exterior este de 1 / n rev = 360 / n XCT = 2 XCT / n rad. Este mai ușor să înțelegeți acest lucru dacă vă gândiți mai degrabă la revoluții decât la grade (sau radiani). Unghiul interior este suplimentul unghiului exterior.

predarea revoluțiilor, diplomelor și Radianilor
cred că ar fi bine dacă profesorii ar introduce revoluții (viraje) în același timp în care introduc diplome. Acest lucru îi va ajuta pe elevi să înțeleagă unghiurile la un nivel mai fundamental, mai puțin dependent de numărul magic arbitrar 360. Profesorii deja introduce conceptul general de rotații (se transformă), atunci când ei spun lucruri de genul „un cerc complet de 360°”, dar ei pot face conceptul numeric mai precis prin a spune „o rotație completă este de 360°, o jumătate de tură este de 180°, un sfert de rotație este de 90°, și un al optulea rândul său, este de 45°” sau scrie „1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90°, și 1/8 rev = 45°”. Elevii ar trebui să practice ocazional să facă câteva calcule folosind revoluții (viraje), mai degrabă decât grade. Desigur, elevii vor trebui să-și petreacă cea mai mare parte a timpului învățând să calculeze cu grade (și mai târziu, radiani), deoarece acesta este standardul.
unghiuri în trigonometrie și calcul
în cele din urmă, să aruncăm o privire rapidă asupra matematicii mai avansate: trigonometria și calculul.
putem lua în considerare utilizarea revoluțiilor cu funcții trigonometrice (sinus, cosinus, tangentă). De exemplu, în loc de a spune cos(60 int.) = 1/2 sau cos(int./3) = 1/2 folosind radiani, am putea dori să spunem cos (1/6) = 1/2 folosind rotații. Dar acest lucru nu este practic, deoarece depindem de calculatoare pentru a evalua funcțiile trigonometrice, iar calculatoarele au de obicei doar moduri DEG și RAD, nu modul REV.
când mergem la niveluri mai profunde ale matematicii, cum ar fi calculul și analiza matematică, se dovedește că radianii sunt cele mai raționale și naturale unități. De exemplu, luați în considerare această ecuație fundamentală: limita păcatului(x)/x pe măsură ce X se apropie de 0 este exact 1. Această ecuație nu ar fi atât de elegantă dacă am folosi altă unitate decât radianii.