arta fractală reprezintă Alianța artei și matematicii. Această formă de artă recentă folosește computerele pentru a realiza imagini din formule matematice. Arta fractală are un aspect adesea geometric, modele complicate și o multitudine de detalii. Dar cum te duci despre crearea de imagini din formule matematice ?
în primul rând, ce înseamnă „Fractal”?
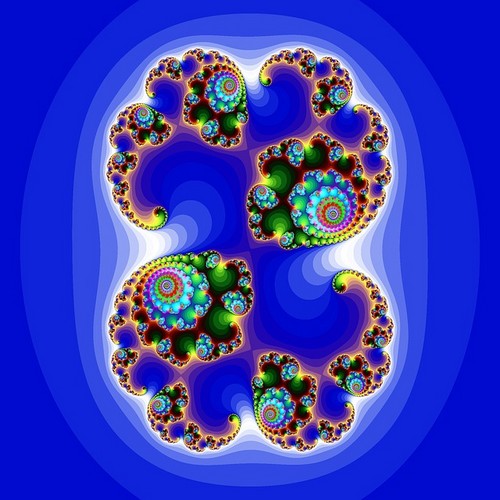
în anii 1970, informaticianul Benoit Mandelbrot a descoperit una dintre cele mai faimoase imagini fractale: setul Mandelbrot.

această descoperire este posibilă prin dezvoltarea computerului, în special datorită puterii de calcul. De asemenea, are loc în contextul științific al dezvoltării teoriei haosului care studiază fenomenele dinamice (turbulență, vârtejuri într-un fluid, oscilație, formă de nor etc.).
de asemenea, geometria fractală se găsește în formele naturii cu contururi complexe (fulg de zăpadă, frunze de copac, formă de nori, vârtejuri, arborescență a rețelei de sânge, forma coastelor maritime etc.) că era greu de înțeles și de modelat cu instrumentele matematice anterioare.

caracteristicile imaginilor fractale
dimensiunea fractală
termenul „fractal” se referă la ideea unei dimensiuni fracționare non-întregi. Până în anii 1960, matematica a studiat obiecte descompuse folosind dimensiuni întregi:
un punct: dimensiunea 0
o linie: dimensiunea 1
un plan: dimensiunea 2
un volum: dimensiunea 3
dar imaginați-vă o foaie de hârtie. Reprezintă un plan, deci are o dimensiune egală cu 2. Dacă zdrobim această foaie, acum ocupă un volum (dimensiunea 3), dar nu este un volum, deoarece nu putem „umple” foaia mototolită cu un material, așa cum s-ar umple un recipient. Prin urmare, dimensiunea foii mototolite este cuprinsă între 2 și 3 : 2.568, de exemplu. O dimensiune fractală ! Obiectele fractale au astfel forme complexe, neregulate, cu contururi pliate și pliate pe ele însele.
auto-similitudine
în ciuda complexității sale, un obiect fractal prezintă detalii similare. Mărirea în interiorul unui fractal arată același model general repetat la scări diferite și în infinit. Prin urmare, o parte este similară cu întregul. Această proprietate se numește invarianță la scară.

tipologie
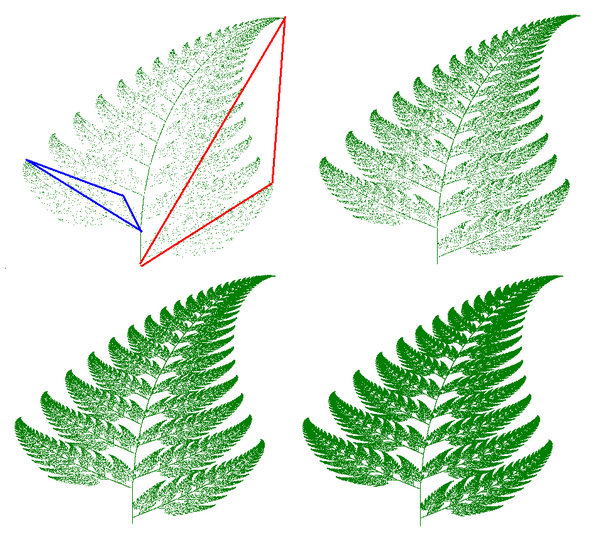
fractali prin recurență

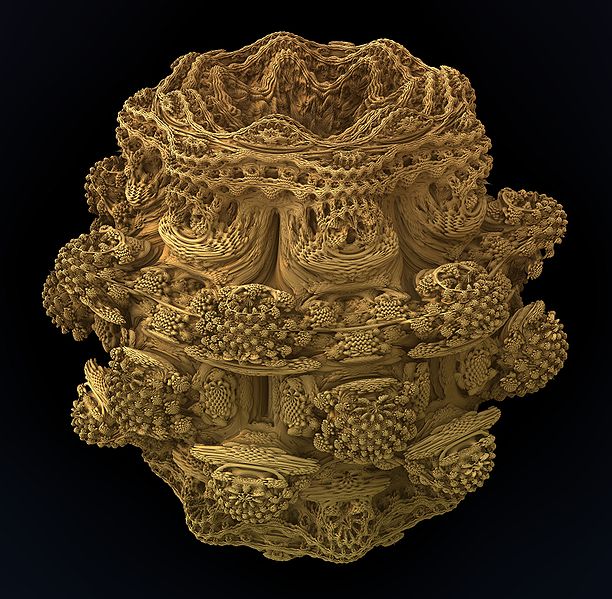
IFS, sisteme de funcții iterate



generarea de imagini fractale,”simplitatea rase complexitate”
construcția de imagini fractale se bazează pe utilizarea algoritmului executat într-o buclă. Este un proces iterativ care repetă o serie de operații simple.
fractali prin recurență
pentru fiecare punct din spațiu, coordonatele punctului sunt trecute într-o ecuație. Rezultatul este apoi alimentat înapoi în aceeași ecuație. Operația se efectuează de mai multe ori la rând (iterații). Apoi testăm rezultatul. Dacă rezultatul tinde spre infinit, atunci punctul de plecare nu este în ansamblu : este colorat în alb. Dacă rezultatul rămâne stabil sau periodic, atunci punctul de plecare este în ansamblu : este colorat negru. Pentru punctele de la graniță, este mai dificil să se determine dacă sunt în set sau în exterior. Apoi este necesar să se efectueze mai multe iterații. În funcție de numărul de iterații necesare pentru a determina punctul, acesta este colorat în nuanțe diferite. Punctele acestei frontiere dau fractalului aspectul său complicat și încurcat.
pentru a desena setul Mandelbrot, folosim numere complexe care reprezintă fiecare un pixel pe plan. Executăm următoarea ecuație pentru fiecare punct : Zn + 1 = Zn2 + C, cu Z0 = 0.
IFS, sisteme de funcții iterate
construcția imaginii se face aici prin copierea în sine. Dar cu fiecare copie, imaginea copiată suferă o transformare geometrică (o transformare liniară reprezentată în matematică de o funcție liniară). Aceste transformări pot fi rotații, aplatizare, forfecare … copiile sunt, de asemenea, contractate înainte de a fi plasate înapoi pe imaginea originală. Procesul se repetă până când se formează o imagine.
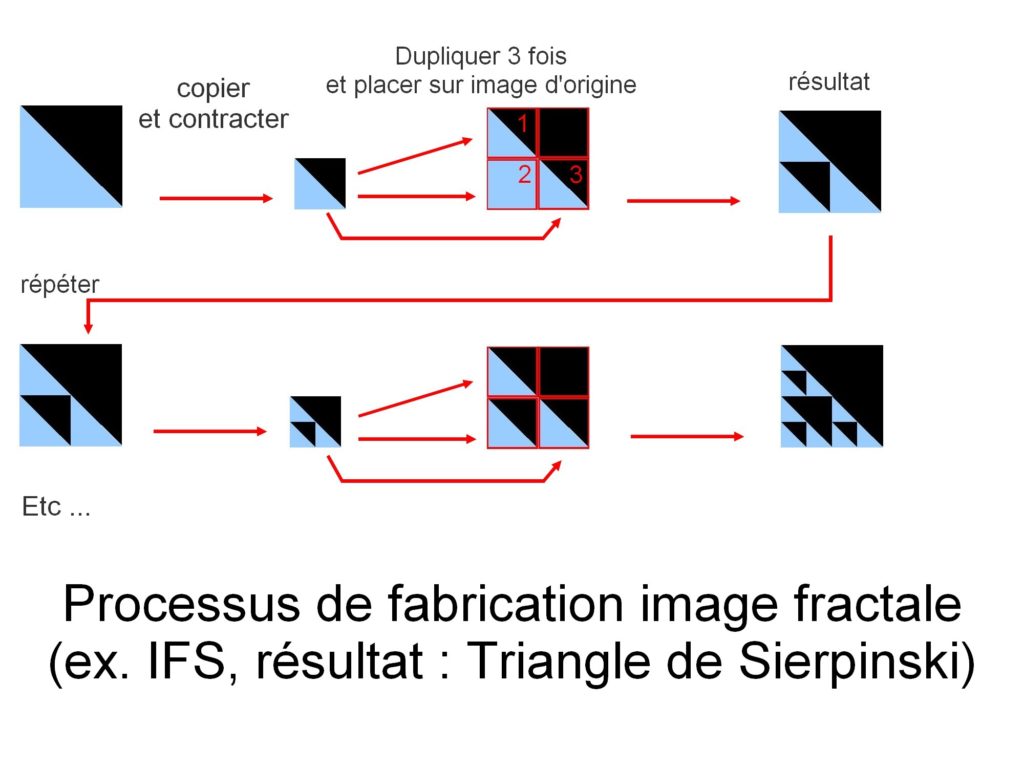
acest exemplu are ca rezultat imaginea triunghiului Sierpinski.
un alt exemplu este generarea fulgului de zăpadă Koch.

IFS poate produce cu ușurință imagini care amintesc de obiecte naturale, cum ar fi copaci, Ferigi etc.