calculând manual un tabel ANOVA cu Python
fundal

analiza varianței, denumită în mod obișnuit ANOVA, este ceva adesea glosat în clasele introductive de statistici. Cu tehnologia de astăzi, este ușor să lăsați computerul să facă toate calculele și să priviți doar valoarea p la sfârșitul unei mese cu aspect ocupat, precum cea de mai sus. În acest articol, voi trece prin ce sunt aceste numere și ce face de fapt ANOVA.
ideea principală din spatele ANOVA este de a testa dacă există o diferență semnificativă statistic în a mijloacele măsurate între subgrupurile unui eșantion. Conceptul datează din jurul anului 1920 cu un statistician britanic pe nume Ronald Fisher, care analiza cantități masive de date privind randamentele culturilor. Fisher a folosit ANOVA pentru a demonstra că există o diferență semnificativă în greutatea medie a cartofilor atunci când s-au folosit diferite îngrășăminte.
pentru a demonstra ANOVA în zilele noastre, mă voi uita la prețurile vinului, mai degrabă decât la greutățile cartofilor. Datele pentru acest exemplu provin din setul de date de revizuire a vinului Kaggle, care conține mii de recenzii despre sticle de vin de la WineEnthusiast. Am filtrat-o până la un subset de 3.000 de recenzii pentru vinurile din Statele Unite, Italia și Franța (1.000 pe țară) și voi folosi ANOVA pentru a testa dacă există o diferență semnificativă statistic în prețul mediu între țările de origine.
un grafic rapid al distribuției prețurilor în funcție de țară arată trei distribuții destul de similare, majoritatea prețurilor fiind în jur de 25 USD pe sticlă.

luând media fiecărei țări, vedem că Franța are cel mai scump vin în medie, urmată de Italia și apoi în cele din urmă de SUA. Dar întrebarea este, este aceasta o diferență reală de preț între țări sau ar putea fi doar din cauza variației eșantionului? Aici intră în joc ANOVA.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
cei patru pași către ANOVA sunt:
1. Formulați o ipoteză
2. Setați un nivel de semnificație
3. Calculați o statistică F
4. Utilizați Statistica F pentru a obține o valoare p
5. Comparați valoarea p și nivelul de semnificație pentru a decide dacă respingeți sau nu ipoteza nulă
formulați o ipoteză
ca și în cazul aproape tuturor testelor de semnificație statistică, ANOVA începe cu formularea unei ipoteze nule și alternative. Pentru acest exemplu, ipotezele sunt următoarele:
ipoteza nulă (H0): Nu există nicio diferență în prețul mediu al vinului între cele trei țări; toate sunt la fel.
ipoteza alternativă (H1): prețul mediu al vinului nu este același între cele trei țări.
Notă, Acesta este un test omnibus, ceea ce înseamnă că, dacă suntem capabili să respingem ipoteza nulă, ne va spune că există o diferență semnificativă statistic undeva între aceste țări, dar nu ne va spune unde este.
Setați un nivel de semnificație
nivelul de semnificație, sau alfa, este probabilitatea de a respinge ipoteza noastră nulă atunci când este de fapt adevărată. În alți termeni, este probabilitatea de a face o eroare de tip I.
de obicei, ar trebui să se cântărească costurile de a face un tip I VS .o eroare de tip II pentru a determina cel mai bun alfa pentru un experiment, dar pentru acest exemplu de jucărie voi folosi doar standardul.05 pentru valoarea noastră de un sfert.
calculați o statistică F
Statistica F este pur și simplu un raport al varianței dintre mijloacele eșantioanelor și varianța din mijloacele eșantionului. Pentru acest test ANOVA, vom analiza cât de departe este prețul mediu al vinului din fiecare țară de prețul mediu global și împărțind acest lucru la cât de mult variația prețului există în distribuția eșantionului fiecărei țări. Formula F-statistică este mai jos, care poate părea complicată până când o descompunem.
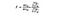
SSB = suma pătratelor între grupuri. Aceasta este însumarea diferenței pătrate dintre media fiecărui grup și media generală de câte ori numărul de elemente pe grup. Pentru acest exemplu, luăm media prețului vinului din fiecare țară, îl scădem din media generală, pătrăm diferența și înmulțim cu 1.000 (numărul de puncte de date pe țară).
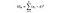
SSW = suma pătratelor din grupuri. Aceasta este însumarea diferenței pătrate dintre media grupului și fiecare valoare din grup. Pentru Franța, am lua prețul mediu al vinului francez, apoi am scădea și pătrat diferența pentru fiecare sticlă de vin francez din cele O mie de puncte de date din acel grup.
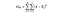
DoFB = grade de libertate între grupuri, pur și simplu numărul de grupuri minus 1. Avem trei țări diferite pe care le comparăm, deci gradele de libertate aici sunt 2.
DoFW = grade de libertate în cadrul grupurilor, pur și simplu numărul de puncte de date minus numărul de grupuri. Avem 3.000 de puncte de date și trei țări diferite, deci acesta este 2.997 pentru acest exemplu.
împărțirea sumei pătratelor pentru un grup la gradele sale de libertate produce pătratele medii pentru acel grup, iar statistica F este doar un raport al pătratelor medii dintre pătratele medii din interior.
mai jos calculez manual aceste valori în Python și ajung la o statistică F de ~4.07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
folosind Statistica F, calculăm o valoare p
odată ce avem Statistica f, o conectăm la o distribuție F pentru a obține o valoare p. Puteți găsi un tabel pentru aceste valori în partea din spate a oricărei cărți de statistici sau există calculatoare online mult mai ușoare care vor face acest lucru pentru dvs. Cu gradele noastre specifice de libertate, o statistică F de 4,07 produce o valoare P.0172.

comparați valoarea p și nivelul de semnificație pentru a decide dacă respingeți sau nu ipoteza nulă
valoarea noastră p înseamnă că presupunând ipoteza nulă (toate țările au același preț mediu al vinului) este adevărată, există aproximativ un 1.7% șanse de a vedea datele pe care le avem prin șansa de eșantionare. Stabilind nivelul nostru de semnificație, sau alfa, la 5% înainte de toate acestea, am spus că am fi dispuși să acceptăm o șansă de 5% de a respinge nulul atunci când este adevărat. Deoarece valoarea noastră p este sub nivelul nostru de semnificație prestabilit, putem respinge ipoteza nulă și putem spune că există o diferență semnificativă statistic în prețul mediu al vinului între țări.
amintiți-vă că ANOVA este un test omnibus, adică pentru că suntem capabili să respingem nul știm că există o diferență între prețurile medii ale vinului între țări, dar nu exact unde. Pentru a afla unde se află diferența, am efectua apoi teste de ipoteză între două țări la un moment dat.
automat ANOVA
ca și cu cele mai multe lucruri în viață, Python are o soluție intuitivă pentru efectuarea ANOVA cu Biblioteca statsmodel. Codul de mai jos face toate calculele din acest articol și scoate un tabel sumar complet cu o statistică F și o valoare P.

Vă mulțumim pentru lectură, codul complet și datele pot fi găsite pe pagina mea GitHub.