Jaka jest najlepsza jednostka miary kątów-obroty, stopnie czy radiany?
obroty
rzadko uczymy się używać najprostszej, najbardziej naturalnej jednostki miary kątów geometrycznych, rewolucji (rev). Inne nazwy tego urządzenia to pełne koło, obrót, pełny obrót i obrót (rot). To wszystkie dobre imiona i wszystkie znaczą to samo.
1 pełne koło = 1 obrot = 1 obrót = 1 rot = 360°
stopnie
w szkole podstawowej dowiadujemy się, że kąty są mierzone w stopniach (°).
1 pełne koło = 360°
radiany
na lekcjach trygonometrii i rachunku różniczkowego w liceum dowiadujemy się, że matematycy wolą radiany (rad).
1 full circle = 2π rad
Uwaga: Jeśli jeszcze nie nauczyłeś się o radianach w szkole, możesz zignorować radiany we wszystkim poniżej.
porównując obroty, stopnie i radiany
porównajmy obroty i stopnie (i radiany).
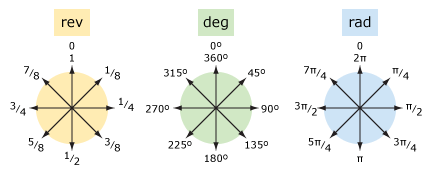
| słowa | rev | deg | rad |
|---|---|---|---|
| no turn | 0 | 0° | 0 |
| quarter turn | 1/4 | 90° | π/2 |
| pół obrotu | 1/2 | 180° | π |
| 3/4 obrotu | 3/4 | 270° | 3π/2 |
| pełny obrót | 1 | 360° | 2π |
| 1/12 | 30° | π/6 | |
| ósma tura | 1/8 | 45° | π/4 |
| szósta tura | 1/6 | 60° | π/3 |
| piąta tura | 1/5 | 72° | 2π/5 |
| trzecia tura | 1/3 | 120° | 2π/3 |
| two turns | 2 | 720° | 4π |
| trzy obroty | 3 | 1080° | 6π |
aby zamienić z obrotów na stopnie, pomnóż przez 360. Aby zamienić ze stopni na obroty, podziel przez 360.
kiedy używasz stopni, często pracujesz z liczbami całkowitymi, ale kiedy używasz obrotów (lub radianów), często pracujesz z ułamkami (lub dziesiętnymi). Obliczenia ręczne są czasami łatwiejsze, gdy używasz obrotów, ale czasami łatwiejsze, gdy używasz stopni. Dobrze wiedzieć w obie strony.
obroty (obroty) są bardziej racjonalną i naturalną jednostką miary niż stopnie. Uzyskasz głębsze zrozumienie kątów, jeśli pomyślisz o obrotach, a nie stopniach. Kąt jest zasadniczo dzieleniem okręgu, a nie sumą stopni. Na przykład kąt prosty jest zasadniczo jedną czwartą okręgu, a nie sumą 90 stopni.
Podzielmy okrąg na N równych sektorów (Patrz diagram poniżej). Kąt każdego sektora wynosi 1 / N rev = 360 / n° = 2π / N rad. Łatwiej jest to zrozumieć, jeśli myślisz o obrotach, a nie stopniach (lub radianach).

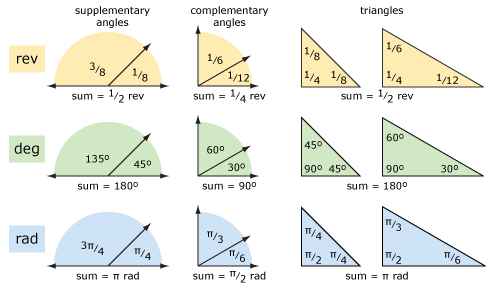
spójrzmy na niektóre podstawowe geometrii za pomocą obrotów i stopni (i radianów). Poniższy diagram pokazuje kąty uzupełniające, kąty uzupełniające i trójkąty. Pojęcia są jaśniejsze, jeśli pomyśli się o obrotach, a nie stopniach. Arytmetyka może być łatwiejsza przy użyciu stopni, jeśli masz problemy z dodawaniem i odejmowaniem ułamków.
spójrzmy na wielokąty (Patrz diagram poniżej). Dla regularnego wielokąta O N bokach kąt zewnętrzny wynosi 1 / N rev = 360 / n° = 2π / N rad. Łatwiej jest to zrozumieć, jeśli myślisz o obrotach, a nie stopniach (lub radianach). Kąt wewnętrzny jest uzupełnieniem kąta zewnętrznego.

Nauczanie obrotów, stopni i radianów
myślę, że byłoby dobrze, gdyby nauczyciele wprowadzali rewolucje (obroty) w tym samym czasie, w którym wprowadzali stopnie. Pomoże to uczniom zrozumieć kąty na bardziej podstawowym poziomie, mniej zależnym od arbitralnej magicznej liczby 360. Nauczyciele wprowadzają już ogólne pojęcie obrotów (obrotów), gdy mówią takie rzeczy jak „pełny okrąg to 360°”, ale mogą uczynić pojęcie bardziej precyzyjnym numerycznie, mówiąc „pełny obrót to 360°, pół obrotu to 180°, ćwierć obrotu to 90°, a ósmy obrót to 45°” lub pisząc „1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90° i 1/8 rev = 45°”. Uczniowie powinni od czasu do czasu ćwiczyć wykonywanie kilku obliczeń za pomocą obrotów (obrotów), a nie stopni. Oczywiście studenci będą musieli spędzać większość czasu na nauce obliczania stopni (a później radianów), ponieważ jest to standard.
kąty w trygonometrii i rachunku różniczkowym
na koniec rzućmy okiem na bardziej zaawansowaną matematykę: trygonometrię i rachunek różniczkowy.
możemy rozważyć użycie obrotów z funkcjami trygonometrycznymi (sinus, cosinus, tangens). Na przykład, zamiast mówić cos (60°) = 1/2 lub cos(π/3) = 1/2 używając radianów, możemy chcieć powiedzieć cos (1/6) = 1/2 używając obrotów. Ale to nie jest praktyczne, ponieważ polegamy na kalkulatorach do oceny funkcji trygonometrycznych, a kalkulatory zwykle mają tylko tryby DEG i RAD, a nie tryb REV.
kiedy przejdziemy do głębszych poziomów matematyki, takich jak rachunek różniczkowy i analiza matematyczna, okazuje się, że radiany są najbardziej racjonalnymi i naturalnymi jednostkami. Na przykład rozważ to podstawowe równanie: granica sin (x) / x przy x dążącym do 0 wynosi dokładnie 1. To równanie nie byłoby tak eleganckie, gdybyśmy używali jednostek innych niż radiany.