Fractal art reprezentuje Sojusz sztuki i matematyki. Ta ostatnia forma sztuki wykorzystuje komputery do tworzenia obrazów z formuł matematycznych. Sztuka fraktalna ma często geometryczny wygląd, skomplikowane wzory i bogactwo szczegółów. Ale w jaki sposób można tworzyć obrazy z formuł matematycznych ?
po pierwsze co oznacza „Fraktal”?
w latach 70.informatyk Benoit Mandelbrot odkrył jeden z najsłynniejszych obrazów fraktalnych: zestaw Mandelbrota.

odkrycie to jest możliwe dzięki rozwojowi komputera, w szczególności dzięki mocy obliczeniowej. Ma to również miejsce w naukowym kontekście rozwoju teorii chaosu, która bada zjawiska dynamiczne (turbulencje, wiry w płynie, oscylacje, kształt chmur itp.).
podobnie geometria fraktalna występuje w kształtach natury o złożonych konturach (Płatek śniegu, liść drzewa, kształt chmur, wiry, arborescencja sieci krwi, kształt wybrzeży morskich itp.), że trudno było zrozumieć i modelować za pomocą poprzednich narzędzi matematycznych.

charakterystyka obrazów fraktalnych
wymiar fraktalny
termin „fraktal” odnosi się do idei nie-całości, wymiaru ułamkowego. Do lat sześćdziesiątych XX wieku matematyka badała obiekty rozkładalne przy użyciu wymiarów całkowitych:
punkt: wymiar 0
linia: Wymiar 1
plan: Wymiar 2
objętość: Wymiar 3
ale wyobraź sobie kartkę papieru. Reprezentuje płaszczyznę, dlatego ma wymiar równy 2. Jeśli zgniatamy ten arkusz, zajmuje on teraz objętość (Wymiar 3), ale nie jest objętością, ponieważ nie możemy „wypełnić” zmiętego arkusza materiałem, tak jak wypełniałby się pojemnik. Wymiar zmiętego arkusza wynosi zatem między 2 a 3: 2,568 na przykład. Fraktalny wymiar ! Obiekty fraktalne mają więc złożone, nieregularne kształty, z konturami złożonymi i złożonymi na siebie.
samopodobieństwo
pomimo swojej złożoności obiekt fraktalny wykazuje podobne szczegóły. Powiększenie fraktala pokazuje ten sam ogólny wzór powtarzany w różnych skalach i w nieskończoność. Część jest więc podobna do całości. Ta właściwość nazywa się niezmienniczością skali.

Typologia
fraktale według powtórzeń

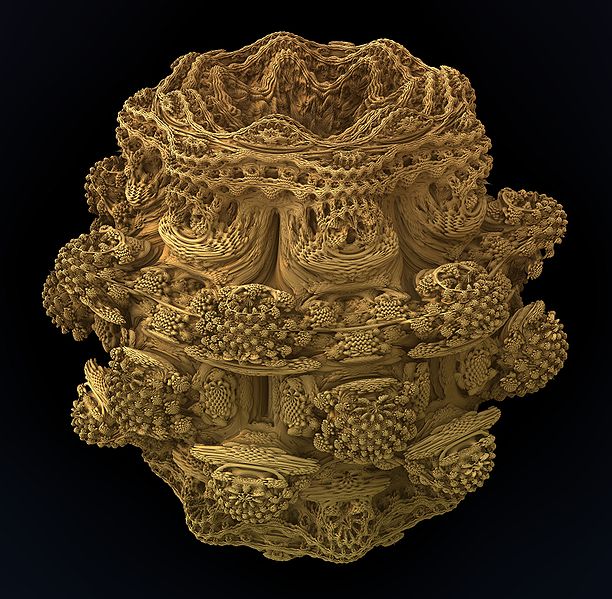
IFS, iteracyjne systemy funkcyjne



generowanie obrazów fraktalnych,”prostota rodzi złożoność”
Budowa obrazów fraktalnych opiera się na wykorzystaniu algorytmu wykonywanego w pętli. Jest to iteracyjny proces powtarzający szereg prostych operacji.
fraktale przez powtarzanie
dla każdego punktu w przestrzeni współrzędne punktu są przekazywane do równania. Wynik jest następnie podawany z powrotem do tego samego równania. Operacja jest wykonywana kilka razy z rzędu (iteracji). Następnie testujemy wynik. Jeśli wynik ma tendencję do nieskończoności, to punkt wyjścia nie jest w całości : jest w kolorze białym. Jeśli wynik pozostaje stabilny lub okresowy, punkt wyjścia jest w całości: jest w kolorze czarnym. W przypadku punktów na granicy trudniej jest określić, czy znajdują się one w zestawie, czy na zewnątrz. Następnie konieczne jest przeprowadzenie większej liczby iteracji. W zależności od liczby iteracji wymaganych do określenia punktu, jest on zabarwiony w różnych odcieniach. Punkty tej granicy nadają fraktalowi jego skomplikowany i splątany wygląd.
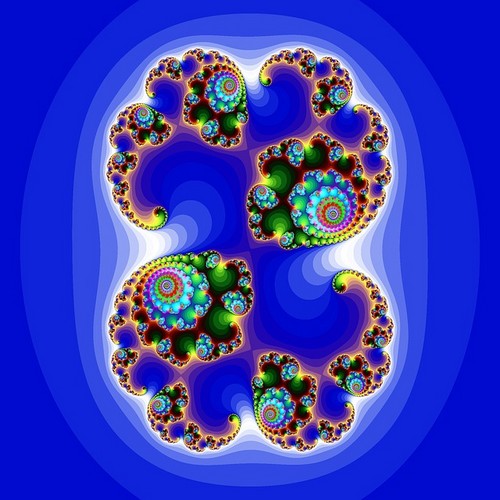
aby narysować zbiór Mandelbrota, używamy liczb zespolonych, z których każda reprezentuje piksel na płaszczyźnie. Dla każdego punktu wykonujemy następujące równanie: Zn + 1 = Zn2 + c, z Z0 = 0.
IFS, iteracyjne systemy funkcyjne
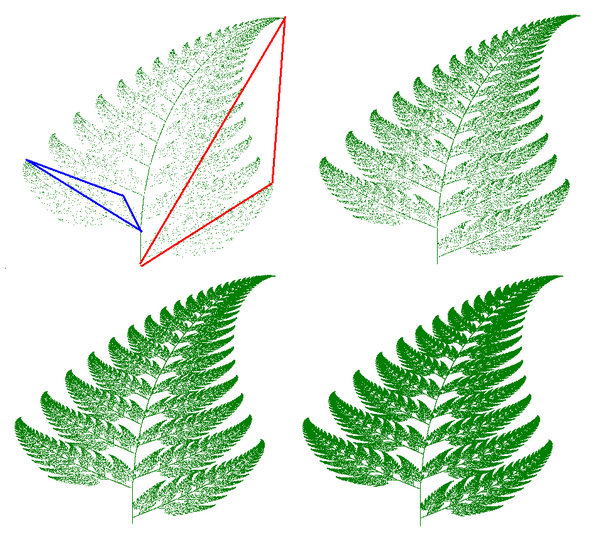
Budowa obrazu odbywa się tutaj poprzez samo kopiowanie. Ale z każdą kopią kopiowany obraz przechodzi transformację geometryczną (przekształcenie liniowe reprezentowane w matematyce przez funkcję liniową). Te przekształcenia mogą być obrotami, spłaszczaniem , ścinaniem … kopie są również zakontraktowane przed umieszczeniem z powrotem na oryginalnym obrazie. Proces ten jest powtarzany do momentu utworzenia obrazu.
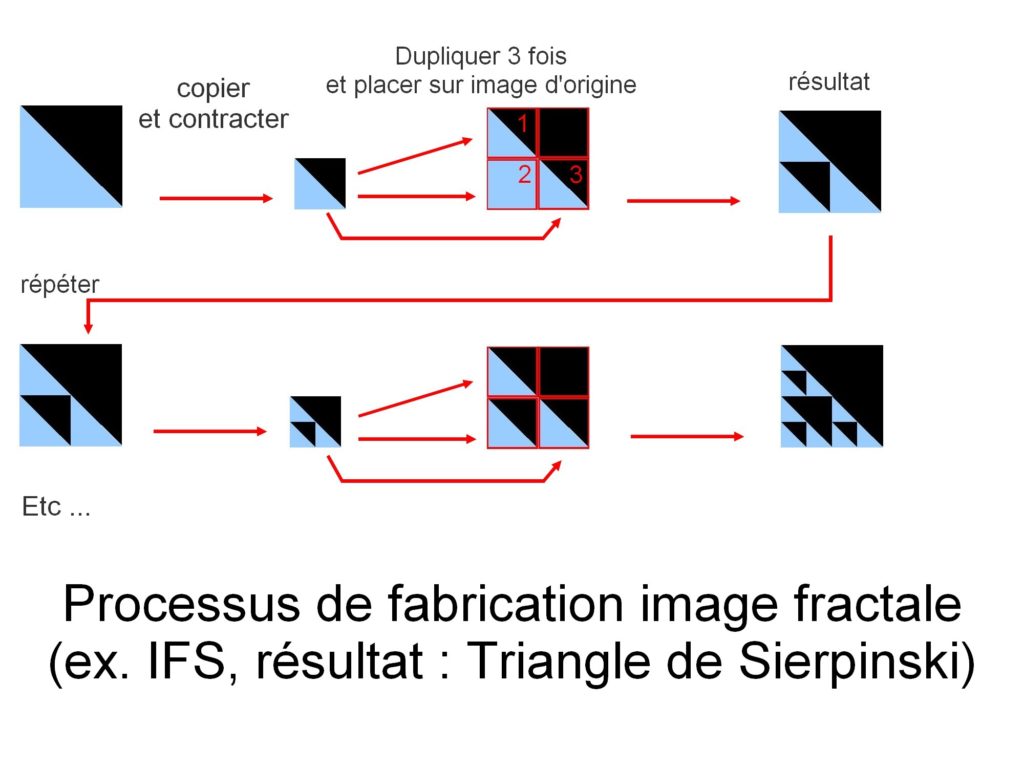
ten przykład daje obraz trójkąta Sierpińskiego.
Innym przykładem jest generacja płatka śniegu Koch.

IFS może z łatwością tworzyć obrazy przypominające obiekty naturalne, takie jak drzewa, paprocie itp.