ANOVA wyjaśnione na przykładzie

Tło

Analiza wariancji, zwykle określana jako ANOVA, jest czymś często omawianym w klasach statystyk wprowadzających. Dzięki dzisiejszej technologii, łatwo jest pozwolić komputerowi wykonać wszystkie obliczenia i po prostu spojrzeć na wartość p na końcu zajętej tabeli, takiej jak ta powyżej. W tym artykule omówię, czym są te liczby i czym właściwie zajmuje się ANOVA.

główną ideą ANOVA jest sprawdzenie, czy istnieje statystycznie istotna różnica w mierzonej średniej między podgrupami próbki. Koncepcja sięga około 1920 roku, kiedy Brytyjski statystyk Ronald Fisher analizował ogromne ilości danych na temat plonów. Fisher użył ANOVA, aby udowodnić, że istniała znacząca różnica w średniej wadze ziemniaków, gdy stosowano różne nawozy.

aby zademonstrować ANOVĘ w dzisiejszych czasach, będę przyglądał się cenom wina, a nie wadze ziemniaków. Dane dla tego przykładu pochodzą z zbioru danych Kaggle ’ s Wine Review, który zawiera tysiące opinii na temat butelek wina z WineEnthusiast. Przefiltrowałem go do podzbioru recenzji 3,000 dla Win ze Stanów Zjednoczonych, Włoch i Francji (1,000 na kraj) i użyję ANOVA do sprawdzenia, czy istnieje statystycznie istotna różnica w średniej cenie między krajami pochodzenia.

szybki Wykres rozkładu cen według kraju pokazuje trzy dość podobne rozkłady, z większością cen około 25 dolarów za butelkę.

biorąc pod uwagę średnią każdego kraju, widzimy, że Francja ma najdroższe wino średnio, następnie Włochy, a następnie USA. Ale pytanie brzmi, czy jest to prawdziwa różnica w cenie między krajami, czy może to być tylko ze względu na różnice w próbce? Tu pojawia się ANOVA.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

cztery kroki do ANOVA to:

1. Sformułować hipotezę
2. Ustaw poziom istotności
3. Oblicz statystykę F
4. Użyj statystyki F, aby uzyskać wartość p
5. Porównaj wartość p i poziom istotności, aby zdecydować, czy odrzucić hipotezę zerową

sformułować hipotezy

podobnie jak w przypadku prawie wszystkich testów istotności statystycznej, ANOVA zaczyna się od sformułowania hipotezy zerowej i alternatywnej. W tym przykładzie hipotezy są następujące:

hipoteza zerowa (H0): Nie ma różnicy w średniej cenie wina między tymi trzema krajami; wszystkie są takie same.
hipoteza Alternatywna (H1): średnia cena wina nie jest taka sama między trzema krajami.

uwaga, jest to test zbiorczy, co oznacza, że jeśli jesteśmy w stanie odrzucić hipotezę zerową, powie nam, że statystycznie istotna różnica istnieje gdzieś między tymi krajami, ale nie powie nam, gdzie ona jest.

Ustaw poziom istotności

poziom istotności, czyli alfa, jest prawdopodobieństwem odrzucenia naszej hipotezy zerowej, gdy faktycznie jest prawdziwa. Innymi słowy, jest to prawdopodobieństwo popełnienia błędu typu I.

zazwyczaj należy zważyć koszty popełnienia błędu typu I vs. typu II, aby określić najlepszą Alfę do eksperymentu, ale dla tego przykładu zabawki po prostu użyję standardu .05 dla naszej wartości α.

Oblicz statystykę F

statystyka F jest po prostu stosunkiem wariancji między środkami próbnymi do wariancji w ramach środków próbnych. W tym teście ANOVA przyjrzymy się, jak daleko jest średnia cena wina w każdym kraju od ogólnej średniej ceny i podzielimy ją przez to, jak duże jest zróżnicowanie ceny w podziale próbki w każdym kraju. Wzór f-statistic jest poniżej, co może wyglądać na skomplikowane, dopóki go nie rozbijemy.

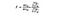
SSB = suma kwadratów między grupami. Jest to sumowanie kwadratowej różnicy między średnią każdej grupy i średnią całkowitą razy liczba elementów w grupie. W tym przykładzie bierzemy średnią z ceny wina każdego kraju, odejmujemy ją od ogólnej średniej, podnosimy do kwadratu różnicę i mnożymy przez 1000 (liczba punktów danych na kraj).

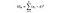
SSW = suma kwadratów w grupach. Jest to sumowanie kwadratowej różnicy między średnią grupy i każdą wartością w grupie. W przypadku Francji przyjęlibyśmy średnią cenę francuskiego wina, a następnie odjęliśmy i do kwadratu różnicę dla każdej butelki francuskiego wina z tysiąca punktów danych w tej grupie.

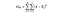
DoFB = stopnie swobody między grupami, po prostu liczba grup minus 1. Porównujemy trzy różne kraje, więc tutaj mamy 2 stopnie swobody.
DoFW = stopnie swobody w obrębie grup, po prostu liczba punktów danych minus liczba grup. Mamy 3000 punktów danych i trzy różne kraje, więc to jest 2997 dla tego przykładu.

podzielenie sumy kwadratów dla grupy przez jej stopnie swobody daje średnie kwadraty dla tej grupy, a statystyka F jest po prostu stosunkiem średnich kwadratów między średnimi kwadratami wewnątrz.

poniżej ręcznie obliczam te wartości w Pythonie i kończę z F-Statistic ~4.07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

używając statystyki F, Oblicz wartość p

gdy już mamy naszą statystykę F, podłączamy ją do dystrybucji F, aby uzyskać wartość P. Możesz znaleźć tabelę dla tych wartości z tyłu dowolnej książki statystyk lub są znacznie łatwiejsze kalkulatory online, które zrobią to za Ciebie. Z naszymi konkretnymi stopniami swobody, Statystyka F wynosząca 4,07 daje wartość P.0172.

Porównaj wartość p i poziom istotności, aby zdecydować, czy odrzucić hipotezę zerową

nasza wartość p oznacza, że zakładając hipotezę zerową(wszystkie kraje mają taką samą średnią cenę wina) jest prawdą, jest mniej więcej 1.7% szans na zobaczenie danych, które mamy przez samą szansę próbkowania. Ustalając nasz poziom istotności, czyli alfa, na 5% Przed tym wszystkim, powiedzieliśmy, że będziemy skłonni zaakceptować 5% szansę odrzucenia null, gdy jest to prawdą. Ponieważ nasza wartość p jest poniżej naszego z góry ustalonego poziomu istotności, możemy odrzucić hipotezę zerową i powiedzieć, że istnieje statystycznie istotna różnica w średniej cenie wina między krajami.

pamiętaj, że ANOVA jest testem zbiorczym, co oznacza, że ponieważ jesteśmy w stanie odrzucić wartość null, wiemy, że istnieje różnica między średnimi cenami wina między krajami, ale nie dokładnie gdzie. Aby dowiedzieć się, gdzie leży różnica, przeprowadzilibyśmy testy hipotez między dwoma krajami naraz.

Automatyczna ANOVA

podobnie jak w przypadku większości rzeczy w życiu, Python ma intuicyjne rozwiązanie do prowadzenia ANOVA z biblioteką statsmodel. Poniższy kod wykonuje wszystkie obliczenia w tym artykule i wyświetla tabelę podsumowującą wraz ze statystyką F i wartością P.

dzięki za przeczytanie, Pełny kod i dane można znaleźć na mojej stronie GitHub.