Wat is de beste maateenheid voor hoeken — omwentelingen, graden of radialen?
omwentelingen
we leren zelden om de eenvoudigste, meest natuurlijke maateenheid voor geometrische hoeken te gebruiken, de omwenteling (rev). Andere namen voor deze eenheid zijn volledige cirkel, draai, volledige draai en rotatie (rot). Dit zijn allemaal goede namen en ze betekenen allemaal hetzelfde.
1 volledige cirkel = 1 omwenteling = 1 omwenteling = 360°
graden
op de basisschool leren we dat hoeken gemeten worden in graden (°).
1 volledige cirkel = 360°
radialen
in de trigonometrie-en calculuslessen op de middelbare school leren we dat wiskundigen de voorkeur geven aan radialen (rad).
1 volledige cirkel = 2π rad
Opmerking: Als u nog niet over radialen op school hebt geleerd, kunt u de radialen in alles hieronder negeren.
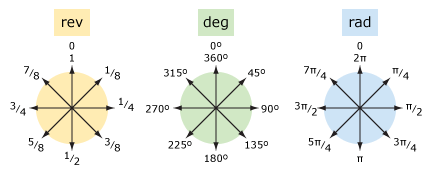
vergelijk omwentelingen, graden en radialen
vergelijk omwentelingen en graden (en radialen).
| woorden | rev | gr | rad |
|---|---|---|---|
| geen beurt | 0 | 0° | 0 |
| kwartslag | 1/4 | 90° | π/2 |
| halve draai | 1/2 | 180° | π |
| drie-kwart draai | 3/4 | 270° | 3π/2 |
| full turn | 1 | 360° | 2π |
| twaalfde beurt | 1/12 | 30° | π/6 |
| achtste beurt | 1/8 | 45° | π/4 |
| zesde beurt | 1/6 | 60° | π/3 |
| vijfde beurt | 1/5 | 72° | 2π/5 |
| derde ronde | 1/3 | 120° | 2π/3 |
| twee bochten | 2 | 720° | 4π |
| drie beurten | 3 | 1080° | 6π |
om van omwentelingen naar graden om te zetten, vermenigvuldig je met 360. Om te converteren van graden naar omwentelingen, delen door 360.
wanneer u Graden gebruikt, werkt u vaak met gehele getallen, maar wanneer u omwentelingen (of radialen) gebruikt, werkt u vaak met breuken (of decimalen). Handberekeningen zijn soms makkelijker als je revoluties gebruikt, maar soms makkelijker als je graden gebruikt. Het is goed om beide kanten te weten.
omwentelingen zijn een meer rationele en natuurlijke maateenheid dan graden. Je krijgt een dieper begrip van hoeken als je denkt aan revoluties in plaats van graden. Een hoek is meer fundamenteel een onderverdeling van een cirkel dan een som van graden. Bijvoorbeeld, een rechte hoek is meer fundamenteel een kwart van een cirkel in plaats van een som van 90 graden.
laten we de cirkel verdelen in n gelijke sectoren (zie diagram hieronder). De hoek van elke sector is 1 / n omw. = 360 / n° = 2π / n rad. Het is makkelijker om dit te begrijpen als je denkt aan revoluties in plaats van graden (of radialen).

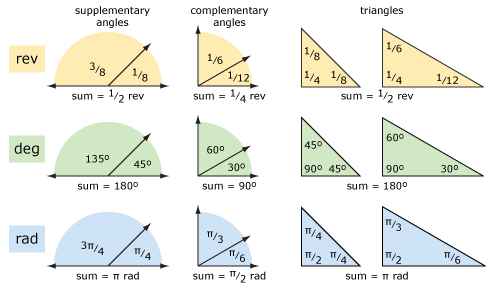
laten we eens kijken naar een aantal fundamentele geometrie met behulp van revoluties en graden (en radialen). Het diagram hieronder toont aanvullende hoeken, complementaire hoeken en driehoeken. De concepten zijn duidelijker als je denkt aan revoluties in plaats van graden. De rekenkunde kan gemakkelijker zijn met graden als je problemen hebt met het optellen en aftrekken van breuken.
laten we eens kijken naar polygonen (zie diagram hieronder). Voor een regelmatige veelhoek met n zijden is de uitwendige hoek 1 / n rev = 360 / n° = 2π / n rad. Het is makkelijker om dit te begrijpen als je denkt aan revoluties in plaats van graden (of radialen). De binnenhoek is het supplement van de buitenhoek.

onderwijs revoluties, graden en radialen
ik denk dat het goed zou zijn als leraren revoluties (bochten) zouden introduceren op hetzelfde moment dat ze graden invoeren. Dit zal de studenten helpen om hoeken te begrijpen op een meer fundamenteel niveau, minder afhankelijk van de willekeurige magische getal 360. Leraren introduceren al het algemene concept van omwentelingen (bochten) als ze dingen zeggen als “een volledige cirkel is 360°”, maar ze kunnen het concept numeriek preciezer maken door te zeggen “een volledige draai is 360°, een halve draai is 180°, een kwart beurt is 90°, en een achtste beurt is 45°” of schrijven “1 omw. = 360°, 1/2 omw. = 180°, 1/4 omw. = 90°, en 1/8 omw. = 45°”. Studenten moeten af en toe oefenen met het doen van een paar berekeningen met behulp van revoluties (bochten) in plaats van graden. Natuurlijk moeten studenten het grootste deel van hun tijd besteden aan het leren berekenen met graden (en later radialen), want dat is de standaard.
hoeken in trigonometrie en Calculus
ten slotte, laten we eens een snelle blik op meer geavanceerde wiskunde: trigonometrie en calculus.
we kunnen het gebruik van omwentelingen met trigonometrische functies (sinus, cosinus, raaklijn) overwegen. Bijvoorbeeld, in plaats van te zeggen cos (60°) = 1/2 of cos(π/3) = 1/2 met behulp van radialen, zouden we kunnen zeggen cos(1/6) = 1/2 met behulp van omwentelingen. Maar dit is niet praktisch omdat we afhankelijk zijn van rekenmachines om de trigonometrische functies te evalueren, en rekenmachines hebben meestal alleen DEG-en RAD-modi, niet de TOERENTALMODUS.
wanneer we naar diepere niveaus van de wiskunde gaan, zoals calculus en wiskundige analyse, blijkt dat radialen de meest rationele en natuurlijke eenheden zijn. Denk bijvoorbeeld aan deze fundamentele vergelijking: de limiet van sin (x)/x als x nadert 0 is precies 1. Deze vergelijking zou niet zo elegant zijn als we een andere eenheid dan radialen gebruiken.