ANOVA Uitgelegd door een Voorbeeld

Achtergrond

variantie-Analyse, doorgaans aangeduid als ANOVA, is iets wat vaak verdoezeld in de inleidende statistiek klassen. Met de technologie van vandaag is het gemakkelijk om de computer alle berekeningen te laten doen en gewoon naar de p-waarde te kijken aan het einde van een druk uitziende tabel zoals hierboven. In dit artikel ga ik door wat deze getallen zijn en wat ANOVA eigenlijk doet.

het belangrijkste idee achter ANOVA is om te testen of er een statistisch significant verschil is in de gemeten gemiddelden tussen subgroepen van een monster. Het concept dateert uit rond 1920 met een Britse statisticus genaamd Ronald Fisher, die was het analyseren van enorme hoeveelheden gegevens over gewasopbrengsten. Fisher gebruikte ANOVA om te bewijzen dat er een significant verschil was in het gemiddelde gewicht van aardappelen wanneer verschillende meststoffen werden gebruikt.

om ANOVA in de huidige tijd aan te tonen, zal ik kijken naar de prijzen van wijn in plaats van het gewicht van aardappelen. De gegevens voor dit voorbeeld zijn afkomstig uit Kaggle ‘ s Wine Review dataset, die duizenden reviews bevat over flessen wijn van WineEnthusiast. Ik heb het gefilterd tot een subset van 3000 beoordelingen voor wijnen uit de Verenigde Staten, Italië en Frankrijk (1.000 per land) en zal ANOVA gebruiken om te testen of er een statistisch significant verschil in de gemiddelde prijs tussen landen van herkomst.

een kort overzicht van de prijsdistributie per land toont drie vrij vergelijkbare verdelingen, met het merendeel van de prijzen rond de $ 25 per fles.

aan de hand van het gemiddelde van elk land zien we dat Frankrijk gemiddeld De duurste wijn heeft, gevolgd door Italië en uiteindelijk de VS. Maar de vraag is, is dit een echt prijsverschil tussen landen of kan dit gewoon te wijten zijn aan steekproefvariatie? Dit is waar ANOVA in het spel komt.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

de vier stappen naar ANOVA zijn:

1. Formuleer een hypothese
2. Stel een significantieniveau in
3. Bereken een F-statistiek
4. Gebruik de F-statistiek om een p-waarde
5 af te leiden. Vergelijk de p-waarde en het significantieniveau om te beslissen of de nulhypothese

wordt afgewezen formuleer een hypothese

zoals bij bijna alle statistische significantietests, begint ANOVA met het formuleren van een nulhypothese en alternatieve hypothese. Voor dit voorbeeld zijn de hypothesen als volgt:

nulhypothese (H0): Er is geen verschil in de gemiddelde wijnprijs tussen de drie landen; ze zijn allemaal hetzelfde.
alternatieve hypothese (H1): De gemiddelde prijs van wijn is niet gelijk tussen de drie landen.

Opmerking, Dit is een omnibus test, wat betekent dat als we in staat zijn om de nulhypothese te verwerpen, het ons zal vertellen dat er een statistisch significant verschil bestaat ergens tussen deze landen, maar het zal ons niet vertellen waar het is.

Stel een significantieniveau in

het significantieniveau, of alfa, is de kans om onze nulhypothese af te wijzen als het waar is. In andere termen, Het is de kans op het maken van een type I fout.

normaal gesproken zou men de kosten van het maken van een type I VS. Een type II fout moeten wegen om de beste alpha voor een experiment te bepalen, maar voor dit speelgoedvoorbeeld ga ik gewoon de standaard gebruiken .05 voor onze α-waarde.

Bereken een F-statistiek

de F-statistiek is gewoon een verhouding tussen de variantie tussen de gemiddelden van de monsters en de variantie binnen de gemiddelden van de monsters. Voor deze ANOVA-test, zullen we kijken naar hoe ver de gemiddelde wijnprijs van elk land is van de totale gemiddelde prijs, en delen dat door hoeveel variatie in prijs er is in de steekproefdistributie van elk land. De F-statistische formule staat hieronder, wat ingewikkeld kan lijken totdat we het opsplitsen.

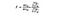
SSB = kwadratensom tussen groepen. Dit is de som van het kwadraatverschil tussen het gemiddelde van elke groep en het totale gemiddelde maal het aantal elementen per groep. In dit voorbeeld nemen we het gemiddelde van de wijnprijs van elk land, trekken deze af van het totale gemiddelde, kwadrateren het verschil en vermenigvuldigen met 1.000 (het aantal datapunten per land).

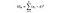
SSW = som van kwadraten binnen groepen. Dit is de som van het kwadraatverschil tussen het groepsgemiddelde en elke waarde in de groep. Voor Frankrijk zouden we de gemiddelde prijs van de Franse wijn nemen, dan het verschil voor elke fles Franse wijn van de duizend datapunten in die groep aftrekken en kwadrateren.

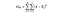
DoFB = vrijheidsgraden tussen groepen, gewoon het aantal groepen min 1. We hebben drie verschillende landen die we vergelijken, dus de vrijheidsgraden hier is 2.
DoFW = vrijheidsgraden binnen groepen, gewoon het aantal datapunten minus het aantal groepen. We hebben 3.000 datapunten en drie verschillende landen, dus dit is 2.997 voor dit voorbeeld.

het delen van de som van kwadraten voor een groep door de vrijheidsgraden geeft de gemiddelde kwadraten voor die groep, en de F-statistiek is gewoon een verhouding van de gemiddelde kwadraten tussen over de gemiddelde kwadraten binnen.

hieronder bereken ik deze waarden handmatig in Python, en eindig met een F-statistiek van ~ 4,07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

met behulp van de F-statistiek, berekenen we een p-waarde

zodra we onze F-statistiek hebben, steken we het in een F-distributie om een p-waarde te krijgen. U kunt een tabel voor deze waarden vinden in de achterkant van een statistisch boek of er zijn veel eenvoudiger online rekenmachines die dit voor u doen. Met onze specifieke vrijheidsgraden levert een F-statistiek van 4.07 een p-waarde op .0172.

vergelijk de p-waarde en het significantieniveau om te beslissen of de nulhypothese

al dan niet wordt afgewezen onze p-waarde betekent dat als de nulhypothese (alle landen hebben dezelfde gemiddelde prijs van wijn) waar is, er ruwweg een 1 is.7% kans op het zien van de gegevens die we hebben door pure steekproefkans. Door ons significantieniveau, of alfa, in te stellen op 5% voor dit alles, zeiden we dat we bereid zouden zijn om een 5% kans te accepteren om de nul te verwerpen als het waar is. Aangezien onze p-waarde onder ons vooraf bepaalde significantieniveau ligt, kunnen we de nulhypothese afwijzen en zeggen dat er een statistisch significant verschil is in de gemiddelde prijs van wijn tussen landen.

onthoud dat ANOVA een omnibus-test is, wat betekent dat we, omdat we de nul kunnen verwerpen, weten dat er een verschil bestaat tussen de gemiddelde wijnprijzen tussen landen, maar niet precies waar. Om uit te vinden waar het verschil ligt, zouden we vervolgens hypothesetests uitvoeren tussen twee landen tegelijk.

automatische ANOVA

zoals met de meeste dingen in het leven, heeft Python een intuïtieve oplossing voor het uitvoeren van ANOVA met de statsmodel-bibliotheek. De onderstaande code doet alle berekeningen in dit artikel en geeft een overzichtstabel compleet met een F-statistiek en p-waarde.

Bedankt voor het lezen, volledige code en gegevens zijn te vinden op mijn GitHub pagina.