Fraktal kunst representerer alliansen av kunst og matematikk. Denne siste kunstformen bruker datamaskiner til å lage bilder fra matematiske formler. Fractal kunst har et ofte geometrisk utseende, intrikate mønstre og et vell av detaljer. Men hvordan går du om å lage bilder fra matematiske formler ?
Først av alt, hva betyr «Fraktal»?
på 1970-tallet oppdaget datavitenskaperen Benoit Mandelbrot et av De mest berømte fraktalbildene: Mandelbrot-settet.

denne oppdagelsen er gjort mulig ved utvikling av datamaskinen, særlig takket være datakraft. Det foregår også i den vitenskapelige konteksten av Utviklingen Av Kaosteorien som studerer dynamiske fenomener(turbulens, hvirvler i væske, svingning, skyform, etc.).
på samme måte finnes fraktal geometri i naturens former med komplekse konturer (snøfnugg, blad av et tre, form av skyer, eddier, arborescence av blodnettverket, form av maritime kyster, etc.) at det var vanskelig å forstå, og å modellere med de tidligere matematiske verktøyene.

Kjennetegn på fraktalbilder
fraktaldimensjonen
begrepet «fraktal» refererer til ideen om en ikke-hel, fraksjonell dimensjon. Fram til 1960-tallet studerte matematikk nedbrytbare objekter ved hjelp av heltallsdimensjoner:
et punkt: dimensjon 0
en linje: dimensjon 1
en plan: dimensjon 2
et volum: dimensjon 3
men tenk deg et ark. Det representerer et plan, derfor har en dimensjon lik 2. Hvis vi smuldrer dette arket, opptar det nå et volum (dimensjon 3), men er ikke et volum fordi vi ikke kan «fylle» det krøllete arket med et materiale som man ville fylle en beholder. Dimensjonen av det krøllete arket er derfor mellom 2 og 3: 2.568 for eksempel. En fraktal dimensjon ! Fraktalobjekter har dermed komplekse, uregelmessige former, med konturer foldet og brettet inn på seg selv.
selvlikhet
Til tross for kompleksiteten viser et fraktalobjekt lignende detaljer. Zooming inne i en fraktal viser det samme generelle mønsteret gjentatt på forskjellige skalaer,og inn i uendelig. En del er derfor lik hele. Denne egenskapen kalles skala invariance.

Typologi
Fraktaler etter gjentakelse

IFS, iterated funksjoner systemer



generering av fraktalbilder, «Enkelhet raser kompleksitet»
konstruksjonen av fraktalbilder er basert på Bruk Av Algoritme utført i en løkke. Det er en iterativ prosess som gjentar en rekke enkle operasjoner.
Fraktaler ved gjentakelse
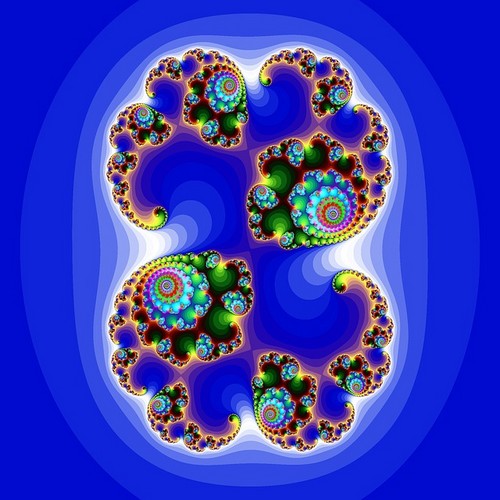
for hvert punkt i rommet sendes koordinatene til punktet inn i en ligning. Resultatet blir deretter matet tilbake i samme ligning. Operasjonen utføres flere ganger på rad (iterasjoner). Så tester vi resultatet. Hvis resultatet har en tendens til uendelig, er utgangspunktet ikke i det hele tatt: det er farget hvitt. Hvis resultatet forblir stabilt eller periodisk, er utgangspunktet i det hele tatt: det er farget svart. For poeng på grensen er det vanskeligere å avgjøre om de er i settet eller utenfor. Det er da nødvendig å utføre flere iterasjoner. Avhengig av antall iterasjoner som kreves for å bestemme punktet, er det farget i forskjellige nyanser. Poengene i denne grensen gir fraktalet sitt kompliserte og sammenflettede utseende.
for å tegne Mandelbrot-settet bruker vi komplekse tall som hver representerer en piksel på flyet. Vi utfører følgende ligning for hvert punkt: Zn + 1 = Zn2 + C, Med Z0 = 0.
ifs, iterated functions systems
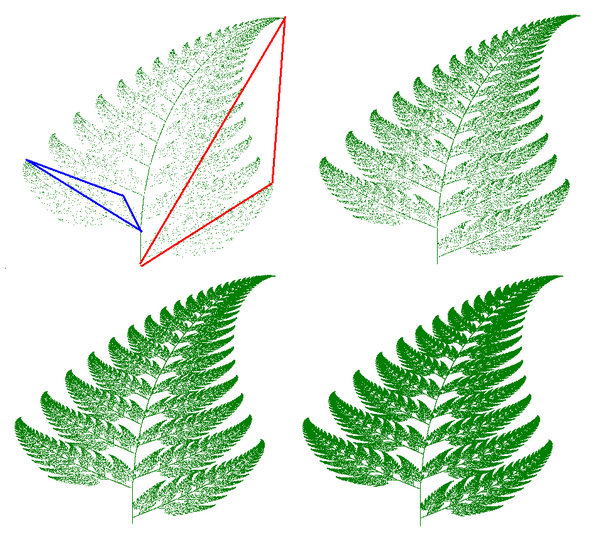
bildekonstruksjon gjøres her ved å kopiere seg selv. Men med hver kopi gjennomgår det kopierte bildet en geometrisk transformasjon (en lineær transformasjon representert i matematikk ved en lineær funksjon). Disse transformasjonene kan være rotasjoner, flattning, skjæring … kopiene er også kontrahert før de plasseres tilbake på originalbildet. Prosessen gjentas til et bilde dannes.
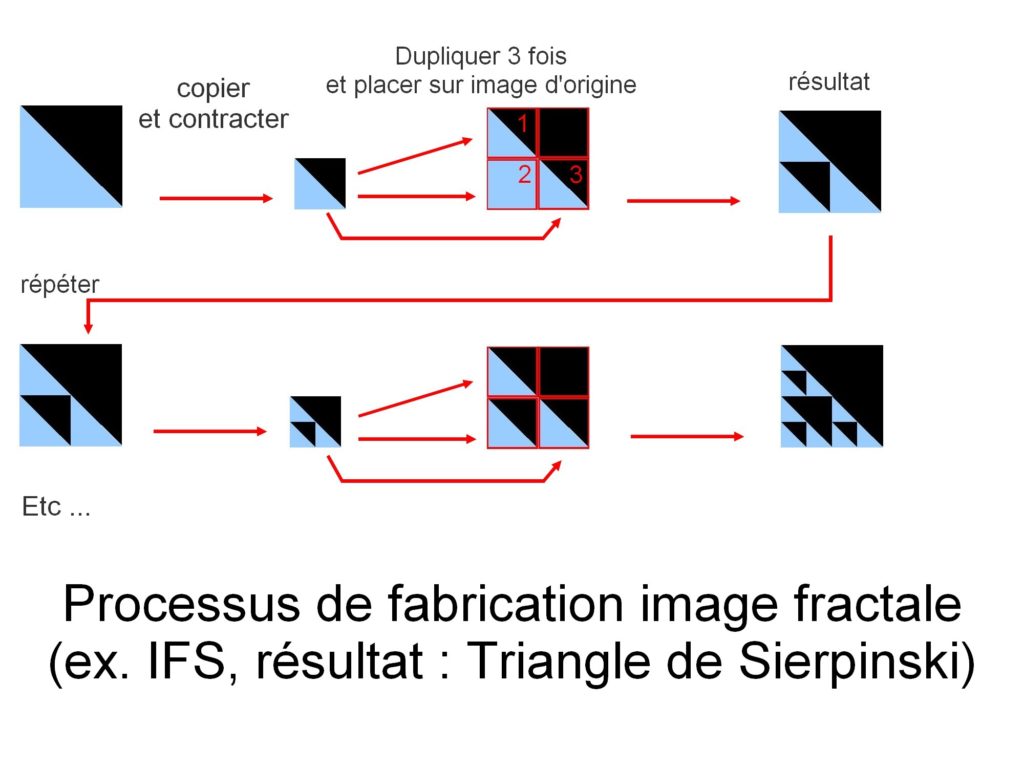
dette eksemplet resulterer i bildet Av sierpinski-trekanten.
Et annet eksempel er generasjonen Av koch-snøfnetten.

IFS kan enkelt produsere bilder som minner om naturlige gjenstander,som trær, bregner, etc.