ANOVA Forklart Med Eksempel

Bakgrunn

Analyse av varians, vanligvis referert TIL SOM ANOVA, er noe ofte glattet over i innledende statistikk klasser. Med dagens teknologi er det enkelt å la datamaskinen gjøre alle beregningene og bare se på p-verdien på slutten av et opptatt bord som det ovenfor. I denne artikkelen vil jeg gå gjennom hva disse tallene er og HVA ANOVA faktisk gjør.

hovedideen BAK ANOVA er å teste om det er en statistisk signifikant forskjell i et målt middel mellom undergrupper av et utvalg. Konseptet går tilbake til rundt 1920 med En Britisk statistiker Ved navn Ronald Fisher, som analyserte massive mengder data om avlinger. Fisher brukte ANOVA til å bevise at det var en signifikant forskjell i gjennomsnittsvekten av poteter når ulike gjødsel ble brukt.

for å demonstrere ANOVA i dag, vil jeg se på prisene på vin i stedet for vekten av poteter. Dataene for dette eksemplet er Fra Kaggles Wine Review datasett, som inneholder tusenvis av anmeldelser på flasker vin Fra WineEnthusiast. Jeg har filtrert det ned til en delmengde på 3000 anmeldelser for viner fra Usa, Italia og Frankrike (1000 per land) og vil bruke ANOVA til å teste om det er en statistisk signifikant forskjell i gjennomsnittsprisen mellom opprinnelseslandene.

et raskt plott av prisfordelingen etter land viser tre ganske like distribusjoner, med flertallet av prisene rundt $ 25 per flaske.

Tar gjennomsnittet av hvert land, ser Vi At Frankrike har den dyreste vinen i gjennomsnitt, etterfulgt Av Italia og så til SLUTT USA. Men spørsmålet er, er dette en ekte prisforskjell mellom land eller kan dette bare skyldes prøvevariasjon? DET ER HER ANOVA kommer inn i spill.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

de fire trinnene TIL ANOVA er:

1. Formuler en hypotese
2. Angi et signifikansnivå
3. Beregn En F-Statistikk
4. Bruk F-Statistikken til å utlede en p-verdi
5. Sammenlign p-verdien og signifikansnivået for å avgjøre om nullhypotesen

Formuler En Hypotese

SOM med nesten alle statistiske signifikansprøver, starter ANOVA med å formulere en null og alternativ hypotese. For dette eksemplet er hypotesene som følger:

Nullhypotesen (H0): Det er ingen forskjell i gjennomsnittsprisen på vin mellom de tre landene; de er alle de samme.
Alternativ Hypotese (H1): gjennomsnittsprisen på vin er ikke den samme mellom de tre landene.

Merk, dette er en omnibustest, noe som betyr at hvis vi er i stand til å avvise nullhypotesen, vil det fortelle oss at en statistisk signifikant forskjell eksisterer et sted mellom disse landene, men det vil ikke fortelle oss hvor det er.

Sett Et Signifikansnivå

signifikansnivået, eller alfa, er sannsynligheten for å avvise nullhypotesen når den faktisk gjelder. I andre termer er det sannsynligheten for Å gjøre En type i-feil.

Vanligvis bør man veie kostnadene ved Å lage En type i vs En TYPE II-feil for å bestemme den beste alfa for et eksperiment, men for dette leketøyeksemplet skal jeg bare bruke standarden .05 for vår α verdi.

Beregn En F-Statistikk

F-statistikken er ganske enkelt et forhold mellom variansen mellom utvalgsmidler og variansen innen utvalgsmidler. FOR DENNE ANOVA-testen ser vi på hvor langt hvert lands gjennomsnittlige vinpris er fra den totale gjennomsnittsprisen, og deler det med hvor mye variasjon i pris det er innenfor hvert lands utvalgsfordeling. F-statistikkformelen er under, som kan se komplisert ut til vi bryter den ned.

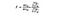
Ssb = Summen av kvadrater mellom grupper. Dette er summasjonen av den kvadrerte forskjellen mellom hver gruppes gjennomsnitt og de samlede middeltider antall elementer per gruppe. For dette eksemplet tar vi gjennomsnittet av hvert lands vinpris, trekker det fra det totale gjennomsnittet, kvadrerer forskjellen og multipliserer med 1000 (antall datapunkter per land).

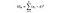
SSW = Summen av kvadrater i grupper. Dette er summen av den kvadrerte forskjellen mellom gruppemiddelverdien og hver verdi i gruppen. For Frankrike ville vi ta den gjennomsnittlige prisen på fransk vin, og deretter trekke og kvadrat forskjellen for hver flaske fransk vin av de tusen datapunktene i den gruppen.

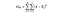
DoFB = Grader av frihet mellom grupper, bare antall grupper minus 1. Vi har tre forskjellige land vi sammenligner, så frihetsgraden her er 2.
DoFW = Frihetsgrader Innenfor Grupper, bare antall datapunkter minus antall grupper. Vi har 3000 datapunkter og tre forskjellige land, så dette er 2997 for dette eksemplet.

Å Dele summen av kvadrater for en gruppe med sine frihetsgrader gir de gjennomsnittlige kvadratene for den gruppen, og f-statistikken er bare et forhold mellom de gjennomsnittlige kvadratene mellom over de gjennomsnittlige kvadratene innenfor.

nedenfor beregner jeg manuelt disse verdiene i Python, og ender med en F-Statistikk på ~4.07.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

bruk F-Statistikken til å beregne en p-verdi

når Vi har F-statistikken, kobler vi den til En f-fordeling for å få en p-verdi. Du kan finne en tabell for disse verdiene på baksiden av noen statistikk bok eller det er langt enklere online kalkulatorer som vil gjøre dette for deg. Med våre spesifikke frihetsgrader gir En F-Statistikk på 4,07 en p-verdi .0172.

Sammenlign p-verdien og signifikansnivået for å avgjøre om du vil avvise nullhypotesen

vår p-verdi betyr at forutsatt at nullhypotesen (alle land har samme middelpris på vin) er sant, er det omtrent en 1.7% sjanse for å se dataene vi har ved ren prøvetaking sjanse. Ved å sette vårt signifikansnivå, eller alfa, på 5% før alt dette, sa vi at vi ville være villige til å akseptere en 5% sjanse for å avvise null når det er sant. Siden vår p-verdi er under vårt forhåndsbestemte signifikansnivå, kan vi avvise nullhypotesen og si at det er en statistisk signifikant forskjell i middelprisen på vin mellom landene.

Husk AT ANOVA er EN omnibus test, noe som betyr at fordi vi er i stand til å avvise null vi vet at en forskjell eksisterer blant de gjennomsnittlige vinprisene mellom land, men ikke akkurat hvor. For å finne hvor forskjellen ligger, vil vi da gjennomføre hypotesetester mellom to land om gangen.

Automatisk ANOVA

Som med de fleste ting i livet, Har Python en intuitiv løsning for å gjennomføre ANOVA med statsmodel library. Koden nedenfor gjør alle beregningene i denne artikkelen og gir en sammendragstabell komplett Med En f-statistikk og p-verdi.

Takk for lesing, full kode og data kan bli funnet på Min GitHub side.