Hvilken er den beste måleenheten for vinkler-omdreininger, grader eller radianer?
Omdreininger
vi lærer sjelden å bruke den enkleste, mest naturlige måleenheten for geometriske vinkler, revolusjonen (rev). Andre navn på denne enheten er full sirkel, sving, full sving og rotasjon (rot). Disse er alle gode navn, og de betyr alle det samme.
1 full sirkel = 1 rev = 1 sving = 1 rot = 360°
Grader
i grunnskolen lærer vi at vinkler måles i grader (°).
1 full sirkel = 360°
Radianer
i videregående trigonometri og kalkulasjonsklasser lærer vi at matematikere foretrekker radianer (rad).
1 full sirkel = 2π rad
Merk: hvis du ennå ikke har lært om radianer i skolen, kan du ignorere radianene i alt under.
Sammenligne Omdreininger, Grader Og Radianer
la oss sammenligne omdreininger og grader (og radianer).
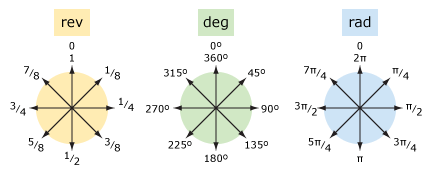
| ord | rev | grader | rad |
|---|---|---|---|
| ingen tur | 0 | 0° | 0 |
| kvart omdreining | 1/4 | 90° | π/2 |
| halv omdreining | 1/2 | 180° | π |
| tre-kvart omdreining | 3/4 | 270° | 3π/2 |
| i full sving | 1 | 360° | 2π |
| tolvte slå | 1/12 | 30° | π/6 |
| åttende tur | 1/8 | 45° | π/4 |
| sjette slå | 1/6 | 60° | π/3 |
| femte slå | 1/5 | 72° | 2π/5 |
| tredje tur | 1/3 | 120° | 2π/3 |
| to omdreininger | 2 | 720° | 4π |
| tre svinger | 3 | 1080° | 6π |
for Å konvertere fra revolusjoner til grader, multiplisere med 360. For å konvertere fra grader til omdreininger, divider med 360.
når du bruker grader jobber du ofte med heltall, men når du bruker omdreininger (eller radianer) jobber du ofte med brøker (eller desimaler). Håndberegninger er noen ganger lettere når du bruker omdreininger, men noen ganger lettere når du bruker grader. Det er godt å vite begge veier.
Omdreininger (svinger) er en mer rasjonell og naturlig måleenhet enn grader. Du får en dypere forståelse av vinkler hvis du tenker på omdreininger i stedet for grader. En vinkel er mer fundamentalt en underavdeling av en sirkel i stedet for en sum av grader. For eksempel er en rett vinkel mer fundamentalt en fjerdedel av en sirkel i stedet for en sum på 90 grader.
la oss dele sirkelen i n like sektorer (se diagram nedenfor). Vinkelen på hver sektor er 1 / n rev = 360 / n° = 2 hryvnias / n rad. Det er lettere å forstå dette hvis du tenker på omdreininger i stedet for grader (eller radianer).

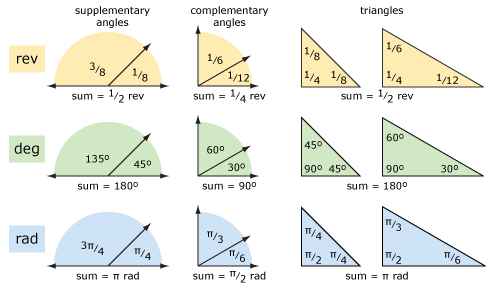
La oss se på noen grunnleggende geometri ved hjelp av omdreininger og grader (og radianer). Diagrammet nedenfor viser supplerende vinkler, komplementære vinkler og trekanter. Begrepene er klarere hvis du tenker på omdreininger i stedet for grader. Aritmetikken kan være lettere å bruke grader hvis du har problemer med å legge til og trekke fraksjoner.
La oss se på polygoner(se diagram nedenfor). For en vanlig polygon med n sider er den utvendige vinkelen 1/n rev = 360/n° = 2π Det er lettere å forstå dette hvis du tenker på omdreininger i stedet for grader (eller radianer). Den indre vinkelen er tillegget til den ytre vinkelen.

Undervisning Revolusjoner, Grader og Radianer
jeg tror det ville være bra hvis lærerne ville innføre revolusjoner (svinger) samtidig som de introduserer grader. Dette vil hjelpe elevene til å forstå vinkler på et mer grunnleggende nivå, mindre avhengig av vilkårlig magisk nummer 360. Lærere som allerede introdusere det generelle konseptet rotasjoner (omdreininger) når de sier ting som «en full sirkel er 360°», men de kan gjøre begrepet mer nøyaktig numerisk ved å si «en full sving er 360°, en halv omdreining er 180°, en kvart omdreining er 90°, og en åttende tur er 45°» eller skriftlig», 1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90°, og 1/8 rev = 45°». Studentene bør av og til øve på å gjøre noen beregninger ved hjelp av omdreininger (svinger) i stedet for grader. Selvfølgelig må studentene bruke mesteparten av tiden på å lære å beregne med grader (og senere radianer), fordi det er standarden.
Vinkler I Trigonometri Og Kalkulator
Til Slutt, La Oss ta en rask titt på mer avansert matematikk: trigonometri og kalkulator.
Vi kan vurdere å bruke omdreininger med trigonometriske funksjoner (sinus, cosinus, tangent). For eksempel, i stedet for å si cos(60°) = 1/2 eller cos(π/3) = 1/2 ved hjelp av radianer, vil vi kanskje si cos (1/6) = 1/2 ved hjelp av omdreininger. Men dette er ikke praktisk fordi vi er avhengige av kalkulatorer for å evaluere trigonometriske funksjoner, og kalkulatorer har vanligvis BARE DEG og RAD moduser, ikke REV-modus.
når vi går til dypere nivåer av matematikk, som kalkulator og matematisk analyse, viser det seg at radianer er de mest rasjonelle og naturlige enhetene. For eksempel, vurder denne grunnleggende ligningen: grensen for synd (x)/x som x nærmer seg 0 er nøyaktig 1. Denne ligningen ville ikke være så elegant hvis vi brukte noen annen enhet enn radianer.