회전,도 또는 라디안과 같은 각도에 가장 적합한 측정 단위는 무엇입니까?
회전
우리는 기하학적 각도에 가장 단순하고 자연스러운 측정 단위를 사용하는 법을 거의 배우지 않는다. 이 장치의 다른 이름은 전체 원,회전,전체 회전 및 회전(썩음)입니다. 이들은 모두 좋은 이름이고 그들은 모두 같은 것을 의미합니다.
1 전체 원=1 회전=1 회전=1 부패= 360°
도
초등학교에서는 각도도(2363)로 측정된다는 것을 배웁니다.
1 개의 가득 차있는 원형= 360°
라디안
고등학교 삼각법 및 미적분 수업에서 우리는 수학자가 라디안을 선호한다는 것을 배웁니다.
1 원=2π rad
참고:지 않은 경우에 대해 배운 라디안 학교에서,당신은 무시할 수 있습니다 라디안에 모든 것을 아래.
회전,도 및 라디안 비교
회전 및도(및 라디안)를 비교합시다.
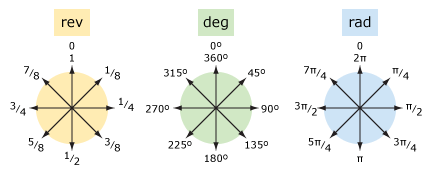
| 말 | rev | deg | rad |
|---|---|---|---|
| 아무 차례 | 0 | 0° | 0 |
| 분기 차례 | 1/4 | 90° | π/2 |
| 반 차례 | 1/2 | 180° | π |
| 분 차례 | 3/4 | 270° | 3π/2 |
| 전체 차례 | 1 | 360° | 2π |
| 두번째 차례 | 1/12 | 30° | π/6 |
| 여덟 번째 차례 | 1/8 | 45° | π/4 |
| 여섯 차례 | 1/6 | 60° | π/3 |
| 다섯 차례 | 1/5 | 72° | 2π/5 |
| 세 번째 차례 | 1/3 | 120° | 2π/3 |
| 두 차례 | 2 | 720° | 4π |
| 세집 | 3 | 1080° | 6π |
변환하에서 회전하도,곱 360. 도에서 회전으로 변환하려면 360 으로 나눕니다.
학위를 사용할 때는 정수로 작업하는 경우가 많지만 회전(또는 라디안)을 사용할 때는 분수(또는 소수)로 작업하는 경우가 많습니다. 당신이 회전하지만 학위를 사용할 때 때로는 쉽게 사용할 때 손 계산은 때때로 쉽다. 두 가지 방법을 모두 아는 것이 좋습니다.
회전(회전)은 도보다 더 합리적이고 자연스러운 측정 단위입니다. 도보다는 회전에 대해 생각하면 각도에 대해 더 깊이 이해할 수 있습니다. 각도는 근본적으로 학위의 합이 아닌 원의 세분입니다. 예를 들어,직각은 근본적으로 90 도의 합이 아닌 원의 1/4 입니다.
원을 엔 등분 섹터(아래 다이어그램 참조). 각 섹터의 각도는 1/엔 레브=360/엔 엔=2,000,000/엔 방사선. 도(또는 라디안)가 아닌 회전에 대해 생각하면 이것을 이해하는 것이 더 쉽습니다.

회전과 각도(및 라디안)를 사용하는 몇 가지 기본 기하학을 살펴 보겠습니다. 아래 다이어그램은 보조 각도,보완 각도 및 삼각형을 보여줍니다. 당신이 회전보다는 정도에 대해 생각하면 개념은 명확하다. 당신은 문제가 추가 및 분수를 뺀 경우 산술도를 사용하여 쉽게 할 수있다.
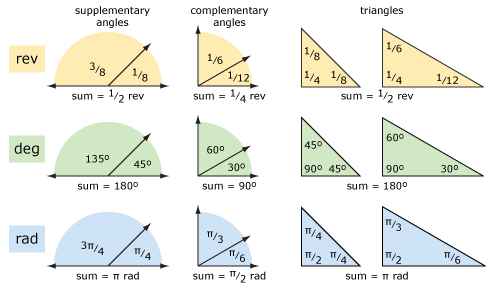
다각형을 살펴 보겠습니다(아래 다이어그램 참조). 예를 들어,이 삼각형의 각도는 삼각형의 각도이며,삼각형의 각도는 삼각형의 각도이며,삼각형의 각도는 삼각형의 각도이며,삼각형의 각도는 삼각형의 각도이며,삼각형의 각도는 삼각형의 각도이며,삼각형의 각도는 삼각형의 각도입니다. 도(또는 라디안)가 아닌 회전에 대해 생각하면 이것을 이해하는 것이 더 쉽습니다. 내부 각도는 외부 각도의 보충입니다.

회전,도,라디안 교육
교사가 회전(회전)을 도입하는 동시에 학위를 도입하면 좋을 것이라고 생각합니다. 이것은 학생들이 임의의 매직 넘버(360)에 덜 의존,보다 근본적인 수준에서 각도를 이해하는 데 도움이 될 것입니다. 교사는 이를 소개한 일반적인 개념의 회전수(회)을 때 그들이 말하는 것 같은”완전한 원 360°”,그러나 만들 수 있습니다 그들은 개념에 더 많은 정확한 숫자적으로 말해서”전체 turn360°,절반을 차례로 180°,설 90°,그리고 여덟 번째 돌 45°”쓰기”1rev=360°,1/2rev=180°,1/4rev=90°1/8rev=45°”. 학생들은 때때로 도가 아닌 회전(회전)을 사용하여 몇 가지 계산을 연습해야합니다. 물론 학생들은 표준이기 때문에 학위(그리고 나중에 라디안)로 계산하는 법을 배우는 데 대부분의 시간을 할애해야합니다.
삼각법 및 미적분의 각도
마지막으로 고급 수학 인 삼각법 및 미적분을 간단히 살펴 보겠습니다.
삼각 함수(사인,코사인,탄젠트)로 회전을 사용하는 것을 고려할 수 있습니다. 예를 들어,말하기 대신 cos(60°)=1/2 또는 cos(π/3)=1/2 를 사용하여 라디안,우리는 말을 할 수 있습니다 cos(1/6)=1/2 를 사용하여혁명을 일으키고 있다. 우리는 삼각 함수를 평가하는 계산기에 의존하기 때문에 그러나 이것은 실용적이지 않다,계산기는 일반적으로 전용도 및 방사선 모드가 아닌 회전 모드가 있습니다.
미적분학 및 수학적 분석과 같은 더 깊은 수준의 수학에 갈 때 라디안이 가장 합리적이고 자연스러운 단위라는 것이 밝혀졌습니다. 예를 들어,이 기본 방정식을 고려하십시오. 라디안 이외의 단위를 사용한다면 이 방정식은 그리 우아하지 않을 것입니다.