角度—回転数、度、ラジアンの最適な測定単位はどれですか?
回転数
私たちは、幾何学的角度のための最も単純な、最も自然な測定単位、回転(rev)を使用することを学ぶことはめったにありません。 この単位の他の名前は完全な円、回転、完全な回転および回転(rot)である。 これらはすべて良い名前であり、彼らはすべて同じことを意味します。
1フルサークル=1回転=1回転=1回転=1回転=1回転=1回転=1回転=1回転=1回転=1回転=1回転=1回転= 360°
度
小学校では、角度は度(°)で測定されることを学びます。
1円= 360°
ラジアン
高校の三角法と微積分のクラスでは、数学者はラジアン(rad)を好むことを学びます。
1full circle=2π rad
注:学校でラジアンについてまだ学んでいない場合は、以下のすべてのラジアンを無視することができます。
回転数、度、ラジアンの比較
回転数と度(およびラジアン)を比較しましょう。
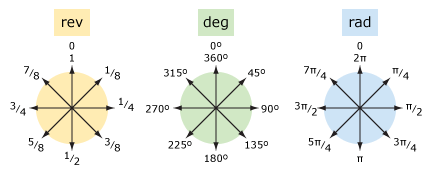
| 言葉 | rev | deg | rad |
|---|---|---|---|
| しばらくは同様の傾向 | 0 | 0° | 0 |
| 四番 | 1/4 | 90° | π/2 |
| 半回転 | 1/2 | 180° | π |
| 四番 | 3/4 | 270° | 3π/2 |
| フル | 1 | 360° | 2π |
| 1/12 | 30° | π/6 | |
| 八番 | 1/8 | 45° | π/4 |
| 六番 | 1/6 | 60° | π/3 |
| 第五回 | 1/5 | 72° | 2π/5 |
| 三番 | 1/3 | 120° | 2π/3 |
| 二巻 | 2 | 720° | 4π |
| 三オ | 3 | 1080° | 6π |
変換からの回転を、増殖による360があります。 度から回転に変換するには、360で除算します。
度を使用するときは整数で作業することがよくありますが、回転(またはラジアン)を使用するときは分数(または小数)で作業することがよくあり 手の計算は、回転数を使用すると簡単になることがありますが、度を使用すると簡単になることがあります。 両方の方法を知っているのは良いことです。
回転数(回転数)は、度よりも合理的で自然な測定単位です。 角度ではなく回転について考えると、角度をより深く理解することができます。 角度は、より基本的には、度の合計ではなく、円の細分化です。 たとえば、直角は、90度の合計ではなく、より基本的には円の四分の一です。
円をn個の等しいセクタに分割しましょう(下の図を参照)。 各セクターの角度は1/n rev=360/n°=2π/n radです。 度(またはラジアン)ではなく回転について考えると、これを理解する方が簡単です。

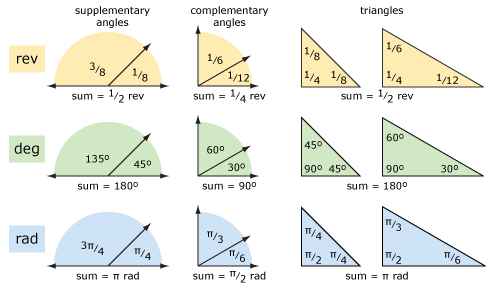
回転と度(およびラジアン)を使用して、いくつかの基本的なジオメトリを見てみましょう。 下の図は、補足角度、補足角度、および三角形を示しています。 あなたが度ではなく回転について考えるならば、概念はより明確です。 分数の加算と減算に問題がある場合は、度を使用して算術演算が簡単になる場合があります。
ポリゴンを見てみましょう(下の図を参照)。 N辺を持つ正多角形の場合、外角は1/n rev=360/n°=2π/n radです。 度(またはラジアン)ではなく回転について考えると、これを理解する方が簡単です。 内角は外角の補足です。

回転数、度、ラジアンを教える
教師が度を導入するのと同時に回転(ターン)を導入するのは良いことだと思います。 これは、学生が任意の魔法数360にあまり依存しない、より基本的なレベルで角度を理解するのに役立ちます。 教師はすでに”完全な円は360°”のようなものを言うときに回転(ターン)の一般的な概念を紹介していますが、”完全な回転は360°、半回転は180°、四分の一回転は90°、八回転は45°”または”1回転=360°、1/2回転=180°、1/4回転=90°、1/8回転=45°”と書くことで、概念をより数値的に正確にすることができます。 学生は時折、度ではなく回転(ターン)を使用していくつかの計算を行う練習をする必要があります。 もちろん、学生は、それが標準であるため、学位(およびそれ以降のラジアン)で計算することを学ぶためにほとんどの時間を費やす必要があります。
三角法と微積分の角度
最後に、より高度な数学、三角法と微積分を簡単に見てみましょう。
三角関数(正弦、余弦、正接)で回転を使用することを検討できます。 たとえば、ラジアンを使用してcos(60°)=1/2またはcos(π/3)=1/2と言う代わりに、回転数を使用してcos(1/6)=1/2と言うことができます。 しかし、三角関数を評価するために電卓に依存しており、電卓は通常、REVモードではなくDEGモードとRADモードしか持たないため、これは実用的ではありません。
微積分や数学的分析などのより深いレベルの数学に行くと、ラジアンは最も合理的で自然な単位であることがわかります。 たとえば、次の基本方程式を考えてみましょう。xが0に近づくにつれてのsin(x)/xの限界は正確に1です。 ラジアン以外の単位を使用した場合、この方程式はそれほどエレガントではありません。