フラクタルアートは、芸術と数学の同盟を表しています。 この最近の芸術形式は、数式から画像を作るためにコンピュータを使用しています。 フラクタルアートは、多くの場合、幾何学的な外観、複雑なパターンと詳細の富を持っています。 しかし、数式から画像を作成するにはどうすればよいですか?
まず、”フラクタル”とはどういう意味ですか?
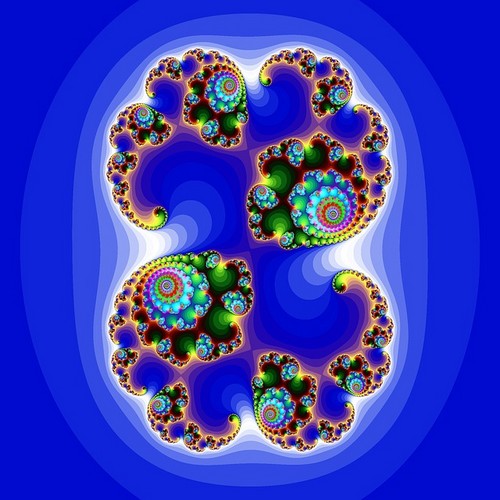
1970年代、コンピュータ科学者ブノワ-マンデルブロは、最も有名なフラクタル画像の一つであるマンデルブロ集合を発見しました。

この発見は、コンピュータの開発、特に計算能力のおかげで可能になりました。 また、動的現象(乱流、流体中の渦、振動、雲の形状など)を研究するカオス理論の開発の科学的文脈でも行われます。).
同様に、フラクタル幾何学は、複雑な輪郭を持つ自然の形(雪片、木の葉、雲の形、渦、血流ネットワークの樹状突起、海上海岸の形など)に見られる。)理解することは困難であり、以前の数学的ツールでモデル化することは困難でした。

フラクタル画像の特徴
フラクタル次元
“フラクタル”という用語は、非全体の分数次元のアイデアを指します。 1960年代まで、数学は整数次元を使用して分解可能なオブジェクトを研究しました:
点:次元0
線:次元1
計画:次元2
体積:次元3
しかし、紙 それは平面を表し、したがって2に等しい次元を有する。 このシートをくしゃくしゃにすると、体積(次元3)を占めますが、容器を満たすようにくしゃくしゃにしたシートを材料で”満たす”ことができないため、体積ではありません。 従ってしわくちゃにされたシートの次元は2と3の間にある:例えば2.568。 フラクタル次元! したがって、フラクタルオブジェクトは複雑で不規則な形をしており、輪郭は折り畳まれて折り畳まれています。
自己相似性
その複雑さにもかかわらず、フラクタルオブジェクトは同様の詳細を示します。 フラクタルの内部にズームすると、同じ全体的なパターンが異なるスケールで繰り返され、無限大に表示されます。 したがって、部分は全体に似ています。 このプロパティはスケール不変性と呼ばれます。

類型学
再帰によるフラクタル

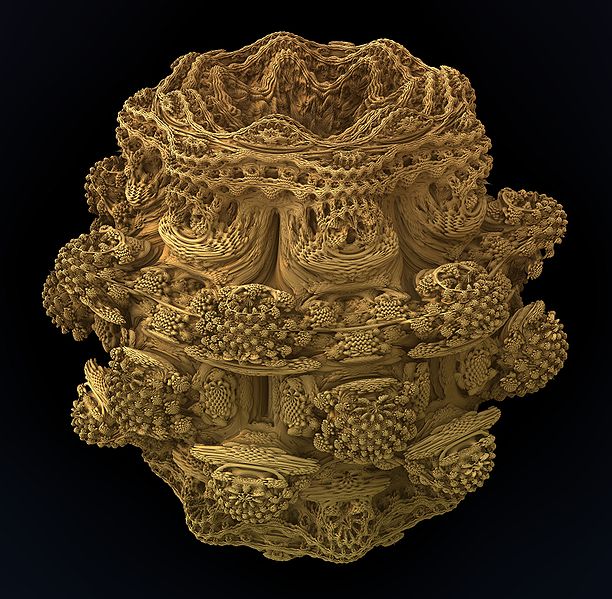
IFS、反復関数システム


フラクタル画像の生成”Simplicity breeds complexity”
フラクタル画像の構築は、ループで実行されるアルゴリズムの使用に基づいています。 これは、一連の簡単な操作を繰り返す反復プロセスです。
再帰によるフラクタル
空間内の各点について、点の座標が方程式に渡されます。 結果は、同じ式にフィードバックされます。 この操作は、連続して数回実行されます(反復)。 次に、結果をテストします。 結果が無限大になる傾向がある場合、開始点は全体ではなく、白に着色されています。 結果が安定している場合、または周期的な場合、出発点は全体にあります:それは黒に着色されています。 境界上の点については、それらが集合内にあるのか外側にあるのかを判断することはより困難である。 その後、より多くの反復を実行する必要があります。 ポイントを決定するために必要な反復回数に応じて、異なる色合いで着色されます。 この境界線のポイントは、フラクタルにその複雑で絡み合った外観を与えます。
マンデルブロ集合を描画するには、それぞれが平面上のピクセルを表す複素数を使用します。 各点について次の式を実行します:Zn+1=Zn2+C、z0=0。
ifs,iterated functions systems
イメージの構築は、ここで自分自身をコピーすることによって行われます。 しかし、各コピーでは、コピーされた画像は幾何学的変換(数学では線形関数で表される線形変換)を受けます。 これらの変換は、回転、平坦化、剪断することができます…コピーも元の画像に戻される前に縮小されます。 このプロセスは、画像が形成されるまで繰り返される。
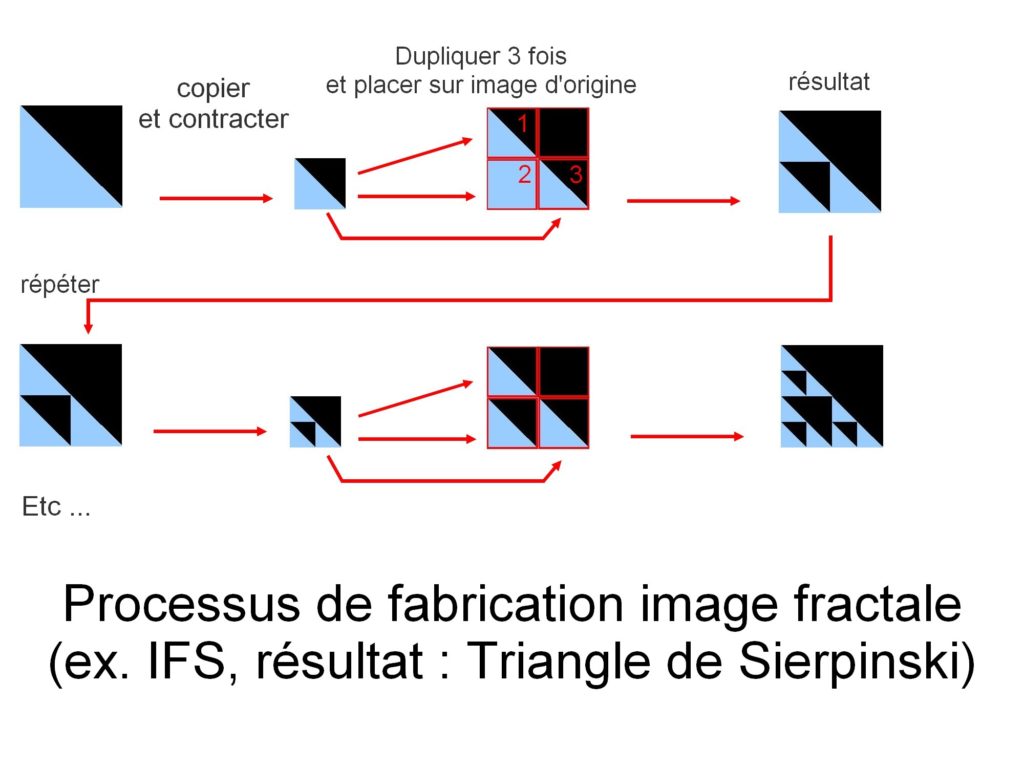
この例では、Sierpinski三角形のイメージが作成されます。
もう一つの例は、コッホの雪片の生成である。

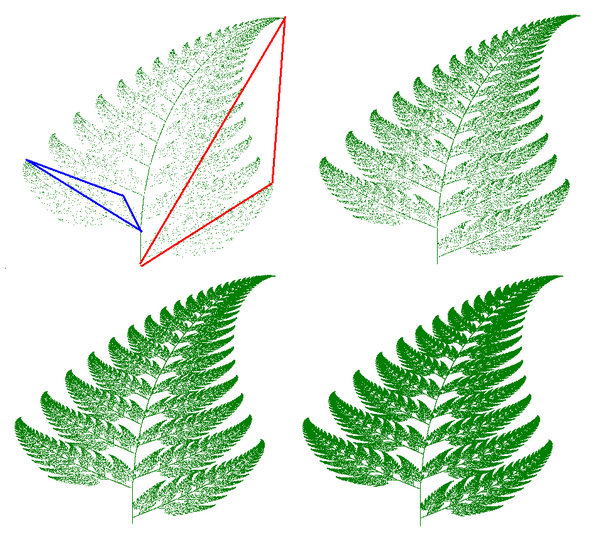
ifsは、木、シダなどの自然の物体を連想させる画像を簡単に生成できます。