Pythonを使用してANOVAテーブルを手動で計算する
背景

分散分析は、一般的にANOVAと呼ばれ、入門統計クラスでよく使われるものです。 今日の技術では、コンピュータがすべての計算を実行し、上のような忙しいテーブルの最後にあるp値を見るのは簡単です。 この記事では、これらの数値とANOVAが実際に何をしているのかを説明します。
ANOVAの背後にある主な考え方は、サンプルのサブグループ間で測定された平均に統計的に有意な差があるかどうかを検定することです。 この概念は、作物収量に関する大量のデータを分析していたRonald Fisherという英国の統計学者との1920年頃にさかのぼります。 FisherはANOVAを使用して、異なる肥料を使用した場合のジャガイモの平均重量に有意差があることを証明しました。
今日のANOVAを実証するために、私はジャガイモの重量ではなくワインの価格を見ていきます。 この例のデータは、WineEnthusiastのワインのボトルに関する何千ものレビューが含まれているKaggleのワインレビューデータセットからのものです。 米国、イタリア、フランスのワインの3,000件のレビュー(国ごとに1,000件)のサブセットにフィルタリングし、ANOVAを使用して、原産国間の平均価格に統計的に有意な差があるかどうかをテストします。
国別の価格分布の簡単なプロットは、3つの非常に類似した分布を示しており、価格の大部分は1ボトルあたり25ドル前後です。

各国の平均を取ると、フランスは平均で最も高価なワインを持っており、イタリア、そして最後に米国が続いていることがわかります。 しかし、問題は、これは国間の価格の本物の違いですか、これはサンプルの変化によるものでしょうか? これがANOVAの出番です。
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
ANOVAへの四つのステップは次のとおりです:
1.
2. 有意水準を設定する
3. F統計量を計算する
4. F統計量を使用して、p値
5を導出します。 P値と有意水準を比較して、帰無仮説を棄却するかどうかを決定する
仮説を定式化する
ほぼすべての統計的有意性検定と同様に、ANOVAは帰無仮説 この例では、仮説は次のとおりです:
帰無仮説(H0): 三国間のワインの平均価格に違いはありません。
対立仮説(H1):ワインの平均価格は3カ国間で同じではない。
注、これはオムニバス検定であり、帰無仮説を棄却できる場合、これらの国の間に統計的に有意な差があることがわかりますが、どこにあるのかはわかりません。
有意水準を設定する
有意水準またはアルファは、それが実際に当てはまるときに帰無仮説を棄却する確率です。 他の言葉では、それはタイプIエラーを起こす確率です。
通常、実験に最適なアルファを決定するには、タイプIとタイプIIのエラーを作成するコストを比較する必要がありますが、このおもちゃの例では、私たちのα値のための05。
F統計量を計算する
F統計量は、単純にサンプル平均間の分散とサンプル平均内の分散の比です。 このANOVA検定では、各国の平均ワイン価格が全体の平均価格からどの程度離れているかを調べ、それを各国のサンプル分布内にある価格の変動で除 F統計式は以下の通りで、分解するまでは複雑に見えるかもしれません。
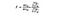
SSB=グループ間の二乗和。 これは、各グループの平均と全体の平均との間の二乗差の合計であり、グループごとの要素数を掛けたものです。 この例では、各国のワイン価格の平均を取り、それを全体の平均から減算し、差を2乗して1,000(国ごとのデータポイント数)を掛けます。
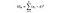
SSW=グループ内の二乗和。 これは、グループ平均とグループ内の各値との間の二乗差の合計です。 フランスの場合、フランスワインの平均価格を取り、そのグループ内の千のデータポイントのフランスワインの各ボトルの差を減算して二乗します。
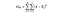
DoFB=グループ間の自由度、単純にグループの数から1を引いたものです。 私たちは比較している三つの異なる国を持っているので、ここでの自由度は2です。
DoFW=グループ内の自由度、単純にデータポイントの数からグループの数を引いたものです。 私たちは3,000のデータポイントと3つの異なる国を持っているので、この例では2,997です。
グループの平方和を自由度で除算すると、そのグループの平均平方が得られ、F統計量は内の平均平方間の平均平方の比率にすぎません。
グループの自以下では、Pythonでこれらの値を手動で計算し、最終的には〜4.07のF統計になります。
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
F統計量を使用して、p値を計算します
F統計量が得られたら、それをF分布に接続してp値を取得します。 あなたは、任意の統計ブックの後ろにこれらの値のテーブルを見つけることができますか、あなたのためにこれを行いますはるかに簡単にオンライ 私たちの特定の自由度では、4.07のF統計量はp値をもたらします。0172.

帰無仮説を棄却するかどうかを決定するためにp値と有意水準を比較する
私たちのp値は、帰無仮説(すべての国が同じワインの平均価私達が薄い見本抽出のチャンスによって持っているデータを見ることの7%のチャンス。 このすべての前に有意水準またはアルファを5%に設定することで、nullがtrueの場合にnullを拒否する5%の可能性を受け入れる意思があると述べました。 私たちのp値は事前に決定された有意水準を下回っているので、帰無仮説を棄却し、国間のワインの平均価格に統計的に有意な差があると言うこと
ANOVAはオムニバス検定であり、nullを拒否できるため、国間の平均ワイン価格に差があることがわかりますが、正確にはどこにあるのかはわかりません。 違いがどこにあるのかを見つけるために、我々は一度に両国間の仮説検定を行います。
自動ANOVA
人生のほとんどのものと同様に、PythonはstatsmodelライブラリでANOVAを実行するための直感的なソリューションを持っています。 以下のコードは、この記事のすべての計算を行い、F統計量とp値を含む要約表を出力します。

読んでくれてありがとう、完全なコードとデータは私のGitHubページで見つけることができます。