a fraktál művészet a művészet és a matematika szövetségét képviseli. Ez a legújabb művészeti forma számítógépeket használ képek készítéséhez matematikai képletekből. A fraktál művészetnek gyakran geometriai megjelenése, bonyolult mintái és rengeteg részlete van. De hogyan lehet képeket készíteni matematikai képletekből ?
először is, mit jelent a” fraktál”?
az 1970-es években Benoit Mandelbrot számítógépes tudós felfedezte az egyik leghíresebb fraktálképet: a Mandelbrot-készletet.

ezt a felfedezést a számítógép fejlesztése teszi lehetővé, különösen a számítási teljesítménynek köszönhetően. A káoszelmélet fejlődésének tudományos összefüggésében is zajlik, amely dinamikus jelenségeket (turbulencia, folyadék örvényei, oszcilláció, felhő alakja stb.).
Hasonlóképpen, a fraktálgeometria megtalálható a természet alakjaiban, összetett kontúrokkal (hópehely, fa levél, felhők alakja, örvények, a vérhálózat arborescenciája, a tengeri partok alakja stb.), hogy nehéz volt megérteni, és modellezni a korábbi matematikai eszközökkel.

a fraktál képek jellemzői
a fraktál dimenzió
a “fraktál” kifejezés egy nem egész, tört dimenzió eszméjére utal. Az 1960-as évekig a matematika bontható objektumokat vizsgált egész dimenziók használatával:
a pont: 0.dimenzió
a vonal: 1. dimenzió
a terv: 2. dimenzió
a kötet: 3. dimenzió
de képzeljünk el egy papírlapot. Síkot képvisel, ezért dimenziója egyenlő 2-vel. Ha összegyűrjük ezt a lapot, akkor most egy kötetet foglal el (3.dimenzió), de nem kötet, mert nem tudjuk “kitölteni” a gyűrött lapot olyan anyaggal, mint egy tartályt. A gyűrött lap mérete tehát például 2 és 3 : 2,568 között van. Egy fraktál dimenzió ! A fraktálobjektumok tehát összetett, szabálytalan formájúak, körvonalakkal, amelyek magukba vannak hajtva.
Önhasonlóság
összetettsége ellenére egy fraktál objektum hasonló részleteket mutat. A fraktál belsejében történő nagyítás ugyanazt az általános mintát mutatja, amely különböző skálákon ismétlődik, a végtelenbe. Egy rész tehát hasonló az egészhez. Ezt a tulajdonságot skála invarianciának nevezzük.

tipológia
fraktálok ismétlődéssel

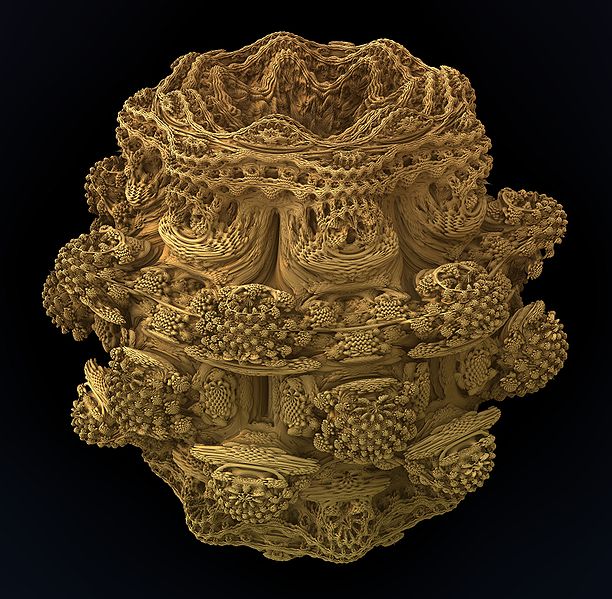
IFS, iterált függvények



fraktál képek generálása,”az egyszerűség komplexitást szül”
a fraktál képek felépítése a hurokban végrehajtott algoritmus használatán alapul. Ez egy iteratív folyamat, amely megismétli az egyszerű műveletek sorozatát.
fraktálok ismétlődéssel
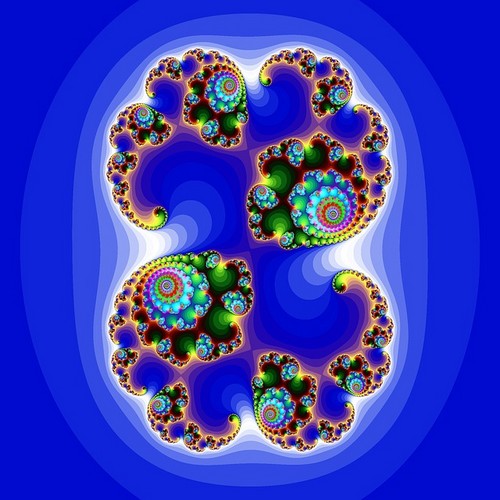
a tér minden egyes pontjára a pont koordinátái átkerülnek egy egyenletbe. Az eredményt ezután visszavezetjük ugyanabba az egyenletbe. A műveletet többször egymás után hajtják végre (iterációk). Ezután teszteljük az eredményt. Ha az eredmény végtelenre hajlik, akkor a kiindulási pont nem az egészben van : fehér színű. Ha az eredmény stabil vagy időszakos marad, akkor a kiindulási pont az egészben van : fekete színű. A határon lévő pontok esetében nehezebb meghatározni, hogy a készletben vagy azon kívül vannak-e. Ezután több iterációt kell végrehajtani. A pont meghatározásához szükséges iterációk számától függően különböző árnyalatokban van színezve. Ennek a határnak a pontjai adják a fraktál bonyolult és kusza megjelenését.
a Mandelbrot-halmaz megrajzolásához komplex számokat használunk, amelyek mindegyike egy pixelt képvisel a síkban. Minden pontra a következő egyenletet hajtjuk végre: Zn + 1 = Zn2 + C, Z0 = 0.
IFS, iterated functions systems
a kép felépítése itt önmagának másolásával történik. De minden másolatnál a másolt kép geometriai átalakuláson megy keresztül (lineáris transzformáció, amelyet a matematikában lineáris függvény képvisel). Ezek az átalakítások lehetnek forgatások, simítások, nyírások … a másolatok is összehúzódnak, mielőtt visszahelyeznék az eredeti képre. A folyamatot addig ismételjük, amíg kép nem képződik.
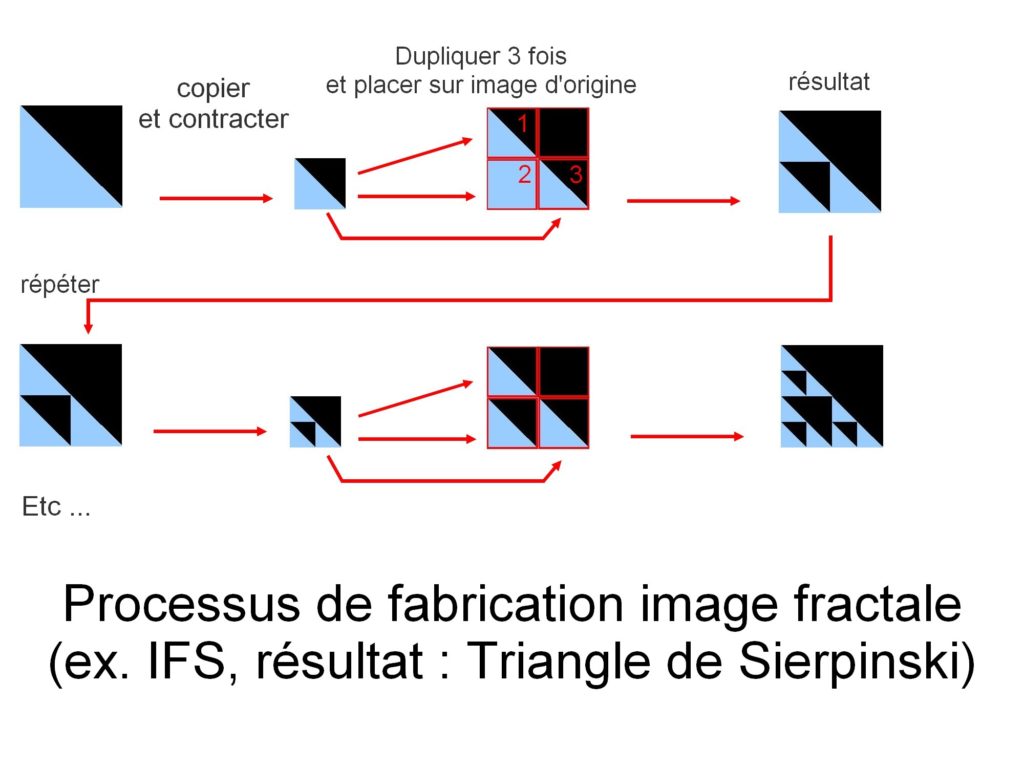
ez a példa a Sierpinski háromszög képét eredményezi.
egy másik példa a Koch hópehely generációja.

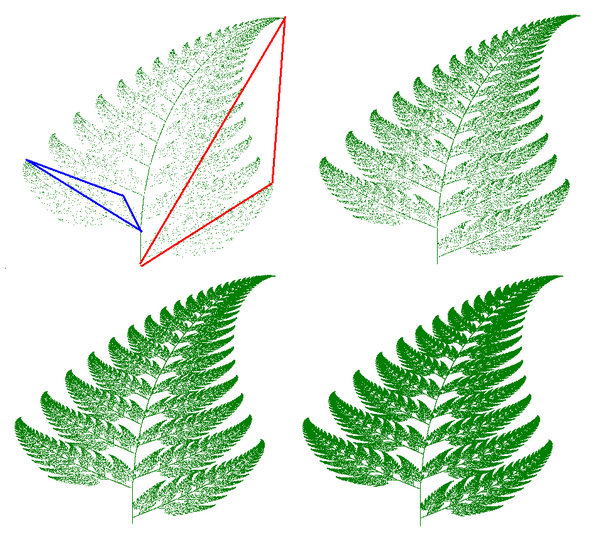
Az IFS könnyen készíthet olyan képeket, amelyek természetes tárgyakra emlékeztetnek, például fákra, páfrányokra stb.