a haranggörbe hasznos grafikon annak összehasonlítására, hogy az adatpontok hogyan viszonyulnak a többi adathoz.
biztos vagyok benne, hogy hallottál már olyan emberekről, akik a haranggörbén alapuló értékelésről beszélnek.
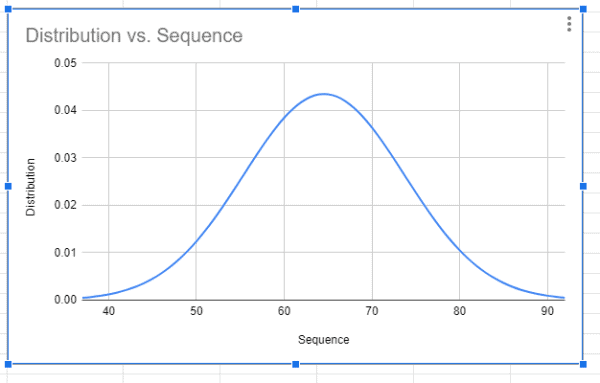
ez a grafikon segít bemutatni, hogy az adatpontok többsége hol található egy grafikonon, milyen közel vannak ezek az adatpontok egymáshoz, és mely adatpontok tekinthetők kiugró értékeknek.
ez az oktatóanyag bemutatja, hogyan hozhat létre haranggörbe-grafikont a Google Táblázatokban egy meglévő adatkészletből.
míg a Sheets rengeteg beépített grafikus eszközzel rendelkezik, néhány számítást kell futtatnia a haranggörbe létrehozásához.
ez a cikk a következőket tartalmazza:
haranggörbe készítése a Google Táblázatokban
a haranggörbe grafikonok általában olyan adatpontokkal működnek a legjobban, amelyek általában közelebb vannak az átlaghoz, mint a szélsőségekhez képest.
példánkban 50 autó-értékelési pontszám hipotetikus listájával fogunk dolgozni.

mielőtt felépítenénk a grafikonunkat, el kell végeznünk néhány számítást:
- Az átlagos (átlagos) érték.
- a szórás értéke (akár populációként, akár mintaként).
- az átlag + / – 3 szórási értéke.
- tartománysorozat.
- az összes adatpont normál eloszlása.
mielőtt elkezdené, hozzon létre egy sor segédoszlopot a grafikon elkészítéséhez szükséges számítások tárolására.

a példában a következő oszlopokat adtam hozzá:
- C: sorrend
- D: Eloszlás
- E: átlagos
- F: szórás
- G: alacsony
- H: Magas
kövesse az alábbi lépéseket, hogy hozzon létre egy haranggörbe grafikon a Google Táblázatok:
- Számítsa ki az átlagos függvény használatához a haranggörbét építő adatok átlagos értékét. A példában az =átlag(B2:B51) képletet használtam az E2 cellában.

- az átlag 64,54-ként tér vissza a példában.
- határozza meg a szórást az =STV képlet segítségével.P () ha dolgozik az összes számot a lakosság vagy = STV.S() ha egy adatmintával dolgozik. A példa a =STDEV képletet használja.S (B1:B51) az F2 cellában, mivel ez csak a rendelkezésre álló autók mintája.

- a szórás 9,1767-ként tér vissza a példában.
- Számítsa ki az átlag alacsony szórási értékét a következő képlettel: =átlag-3*szórás a megfelelő cellákra hivatkozva. A példában az =E2-3*F2 képletet használtam a G2 cellában.

- a példa értéke 37,0098
- Számítsa ki az átlag magas szórási értékét a következő képlettel: =átlag+3*szórás a megfelelő cellákra hivatkozva. A példában az =E2+3*F2 képletet használtam a H2 cellában.

- a példa 92 értéket ad vissza.07
- hozzon létre egy számsorozatot a szekvencia oszlopban a következő képlet segítségével: =szekvencia (magas-alacsony + 1,1, alacsony). A példában a következő képletet használtam: =szekvencia (H2-G2+1,1,G2) a C2 cellában. Ez egész számok sorozatát adja vissza a diagram tartományában.

- ezután számítsa ki az összes adatérték normál eloszlását a norma segítségével.DIST képlet ezzel a mintával: =ArrayFormula (norma.DIST (Adatcellatartomány, átlag, szórás, hamis)). A példában használtam: =ArrayFormula (NORM.DIST(C2: C57,$E$2,$F$2,hamis)) a D2 cellában.

- az összes pontszám eloszlási értékeit adja vissza.
- most végre itt az ideje, hogy elkészítsük a grafikont. A kezdéshez válassza ki az összes értéket a “szekvencia” és az “Eloszlás” oszlopokban.

- nyissa meg a “Beszúrás” menüpontot a fejlécből, és válassza a “diagram” lehetőséget.”

- elemre a diagramszerkesztőben válassza ki a “sima vonaldiagramot” a “beállítás” fül “Diagramtípus” szakaszából.

- A Google Táblázatok mostantól a munkafüzet adatai alapján jelenítik meg a haranggörbe diagramot.

a szélesebb haranggörbe magasabb szórást jelent, míg a magas és vékony haranggörbe alacsonyabb szórást jelent.
mi a haranggörbe és hogyan használják a való életben?
a haranggörbe az értékeloszlás olyan típusa, amelyben az adatpontok az átlaghoz szorosan csoportosulnak.
ezt általában üzleti forgatókönyvekben használják az átlagos adatkészlettől távol eső értékek (mint például a kiugró értékek) megismerésére.
például, ha összehasonlítja egy osztály tanulóinak magasságát, látni fogja, hogy ezeknek a hallgatóknak a többsége közel áll az átlaghoz, néhányuk vagy a haranggörbe jobb oldala (vagyis ezek magasabbak, mint az átlagos hallgató), mások pedig a harangdiagram bal oldalán vannak (vagyis ezek rövidebbek az átlagnál.
tehát, ha olyan kosárlabda csapatot választasz, ahol a magasság előnyt jelent, akkor jobban összpontosíthat a jobb oldali outlier csoport diákjaira.
a haranggörbe grafikonok segítségével bemutathatja a részvénybefektetés, az ingatlanértékek, az osztálytermi osztályzatok, az értékelési pontszámok és sok más olyan adatcsoport adatait, amelyek általában az átlaghoz közeli értékeket konszolidálják.
ez segíthet annak eldöntésében, hogy hol végezzen biztonságos befektetéseket, vagy mi teszi a tisztességes ajánlatot egy ingatlanra.
különösen a haranggörbék hasznosak a felülvizsgálati pontszámok összehasonlításához, mivel az átlagos pontszám gyakran nem a skála középső értéke.
például egy 1-10-es minősítési rendszeren a legtöbb értékelés a 7 körül lebeghet, ami meghatározza az átlagot. Alternatív megoldásként egy olyan áttekintési tétel, amely jelentős mennyiségű kiugró értéket ad vissza a haranggörbéből, nem tekinthető megbízhatónak.
ez az oktatóanyag bemutatja, hogyan hozhat létre haranggörbe-diagramot a Google Táblázatokban. A valós felhasználási esetekben a haranggörbe-diagram létrehozása csak az adatok vizualizálásának és értelmezésének kezdete.
remélem hasznosnak találta ezt az oktatóanyagot!
Egyéb Google Táblázatok oktatóanyagok, amelyek tetszhetnek:
- Hogyan készítsünk kördiagramot a Google Táblázatokban
- Hogyan készítsünk hisztogramot a Google Táblázatokban
- Hogyan készítsünk szórási ábrát a Google Táblázatokban
- Hogyan készítsünk vonaldiagramot a Google Táblázatokban
- gyertyatartó diagram a Google Táblázatokban