ANOVA példával magyarázva

háttér

a varianciaanalízis, amelyet általában ANOVA-nak neveznek, a bevezető statisztikai osztályokban gyakran elkendőzik. A mai technológiával könnyű hagyni, hogy a számítógép elvégezze az összes számítást, és csak nézze meg a P-értéket egy forgalmas kinézetű táblázat végén, mint a fenti. Ebben a cikkben áttekintem, hogy mik ezek a számok, és mit csinál valójában az ANOVA.

az ANOVA fő gondolata annak tesztelése, hogy van-e statisztikailag szignifikáns különbség a mért átlagban a minta alcsoportjai között. A koncepció 1920 körül nyúlik vissza egy Ronald Fisher nevű brit statisztikusnál, aki hatalmas mennyiségű adatot elemzett a terméshozamokról. Fisher az ANOVA segítségével bizonyította, hogy jelentős különbség van a burgonya átlagos tömegében, amikor különböző műtrágyákat használtak.

hogy bemutassam az ANOVA-t a mai napig, inkább a bor árait vizsgálom, mint a burgonya súlyát. A példa adatai a Kaggle Wine Review adatkészletéből származnak, amely több ezer véleményt tartalmaz a WineEnthusiast borosüvegeiről. Leszűrtem az Egyesült Államokból, Olaszországból és Franciaországból származó borok 3000 értékelésének egy részhalmazára (országonként 1000), és az ANOVA segítségével tesztelem, hogy van-e statisztikailag szignifikáns különbség a származási országok közötti átlagos árban.

az országonkénti áreloszlás gyors ábrája három nagyon hasonló eloszlást mutat, az árak többsége üvegenként 25 dollár körül mozog.

az egyes országok átlagát figyelembe véve azt látjuk, hogy átlagosan Franciaországban van a legdrágább bor, amelyet Olaszország, majd végül az Egyesült Államok követ. De a kérdés az, hogy ez valódi árkülönbség-e az országok között, vagy ez csak a minta eltérésének tudható be? Ez az, ahol ANOVA jön a játékba.

wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64

az ANOVA négy lépése a következő:

1. Hipotézis megfogalmazása
2. Állítson be egy szignifikancia szintet
3. Számítson ki egy F-statisztikát
4. Használja az F-statisztikát a p-érték
5 levezetéséhez. Hasonlítsa össze a P-értéket és a szignifikancia szintet annak eldöntéséhez, hogy elutasítja-e a nullhipotézist

hipotézis megfogalmazása

mint szinte minden statisztikai szignifikancia tesztnél, az ANOVA egy nullhipotézis megfogalmazásával kezdődik. Ebben a példában a hipotézisek a következők:

nullhipotézis (H0): A három ország között nincs különbség a bor átlagárában, mindegyik azonos.
alternatív hipotézis (H1): a bor átlagára nem azonos a három ország között.

Megjegyzés: Ez egy omnibusz teszt, ami azt jelenti, hogy ha képesek vagyunk elutasítani a nullhipotézist, akkor azt fogja mondani, hogy statisztikailag szignifikáns különbség létezik valahol ezen országok között, de nem fogja megmondani, hogy hol van.

állítson be szignifikancia szintet

a szignifikancia szint vagy alfa annak a valószínűsége, hogy elutasítjuk nullhipotézisünket, amikor valóban igaz. Más szavakkal, ez az I. típusú hiba elkövetésének valószínűsége.

általában mérlegelni kell az I. típusú vs .típusú hiba elvégzésének költségeit, hogy meghatározzuk a kísérlet legjobb alfáját, de ehhez a játékpéldához csak a szabványt fogom használni.A 05-ös szám a mi számunk.

számítson ki egy F-statisztikát

az F-statisztika egyszerűen a minták közötti variancia aránya a minta átlagán belüli varianciához. Ehhez az ANOVA teszthez megvizsgáljuk, hogy az egyes országok átlagos Borára milyen messze van a teljes átlagártól, és elosztjuk azt azzal, hogy az egyes országok mintaeloszlásán belül mekkora az árváltozás. Az F-statisztikai képlet az alábbiakban található, ami bonyolultnak tűnhet, amíg le nem bontjuk.

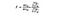
SSB = négyzetek összege csoportok között. Ez a négyzetes különbség összegzése az egyes csoportok átlaga és a csoportonkénti elemek számának összesített átlaga között. Ebben a példában az egyes országok borárának átlagát vesszük, kivonjuk a teljes átlagból, négyzetbe szorozzuk a különbséget, és megszorozzuk 1000-rel (az országonkénti adatpontok száma).

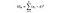
SSW = négyzetek összege csoportokon belül. Ez a csoport átlaga és a csoport minden értéke közötti négyzetes különbség összegzése. Franciaország esetében a francia bor átlagárát vesszük, majd kivonjuk és négyzetre állítjuk az adott csoport ezer adatpontjának minden egyes üveg francia borra vonatkozó különbségét.

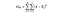
DoFB = a csoportok közötti szabadságfokok, egyszerűen a csoportok száma mínusz 1. Három különböző országot hasonlítunk össze, tehát a szabadság foka itt 2.
DoFW = szabadságfokok csoportokon belül, egyszerűen az adatpontok száma mínusz a csoportok száma. 3000 adatpontunk és három különböző országunk van, tehát ez a példa 2997.

ha egy csoport négyzetének összegét elosztjuk annak szabadságfokaival, akkor az adott csoport átlagos négyzeteit kapjuk, az F statisztika pedig csak az átlagos négyzetek aránya a belül lévő átlagos négyzetek között.

az alábbiakban manuálisan kiszámolom ezeket az értékeket a Pythonban, és az F-statisztika ~4.07 lesz.

Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567

az F-statisztika használatával számítson ki egy p-értéket

Miután megvan az F-statisztikánk, csatlakoztatjuk egy F-eloszláshoz, hogy p-értéket kapjunk. Ezen értékek táblázata megtalálható bármely statisztikai könyv hátulján, vagy vannak sokkal könnyebb online számológépek, amelyek ezt megteszik az Ön számára. A mi sajátos szabadságfokainkkal egy 4,07-es F-statisztika p-értéket ad.0172.

hasonlítsa össze a p-értéket és a szignifikancia szintet annak eldöntéséhez, hogy elutasítja-e a nullhipotézist

p-értékünk azt jelenti, hogy feltételezzük, hogy a nullhipotézis (minden országban azonos a bor átlagára) igaz, nagyjából 1.7% esély arra, hogy puszta mintavételezéssel lássuk a rendelkezésünkre álló adatokat. Azáltal, hogy a szignifikancia szintünket vagy az Alfát 5% – ra állítottuk mindezek előtt, azt mondtuk, hogy hajlandóak vagyunk elfogadni egy 5% – os esélyt a null elutasítására, ha az igaz. Mivel p-értékünk az előre meghatározott szignifikancia szint alatt van, elutasíthatjuk a nullhipotézist, és azt mondhatjuk, hogy statisztikailag szignifikáns különbség van a bor átlagárában az országok között.

ne feledje, hogy az ANOVA egy omnibusz teszt, vagyis mivel képesek vagyunk elutasítani a nullát, tudjuk, hogy különbség van az országok közötti átlagos borárak között, de nem pontosan hol. Ahhoz, hogy megállapítsuk, hol rejlik a különbség, hipotézis teszteket végeznénk egyszerre két ország között.

automatikus ANOVA

mint a legtöbb dolog az életben, Python egy intuitív megoldás vezetésére ANOVA a statsmodel könyvtár. Az alábbi kód elvégzi a cikkben szereplő összes számítást, és egy F-statisztikával és p-értékkel kiegészített összefoglaló táblázatot ad ki.

Köszönöm, hogy elolvastad, a teljes kód és az adatok megtalálhatók a GitHub oldalon.