melyik a legjobb mértékegység szögek-fordulat, fok, vagy radián?
fordulat
ritkán tanuljuk meg a geometriai szögek legegyszerűbb, legtermészetesebb mértékegységét, a forradalmat (rev) használni. A készülék további nevei: full circle, turn, full turn és rotation (rot). Ezek mind jó nevek, és mind ugyanazt jelentik.
1 teljes kör = 1 fordulat = 1 fordulat = 1 rothadás = 360°
fok
az általános iskolában megtanuljuk, hogy a szögeket fokokban mérik (Ft).
1 teljes kör = 360°
Radians
a középiskolai trigonometria és kalkulus osztályok, megtudjuk, hogy a matematikusok inkább radians (rad).
1 full circle = 2 ons rad
Megjegyzés: Ha még nem tanultál radiánokról az iskolában, figyelmen kívül hagyhatod a radiánokat az alábbiakban.
fordulatok, fokok és Radiánok összehasonlítása
hasonlítsuk össze a fordulatokat és a fokokat (és a radiánokat).
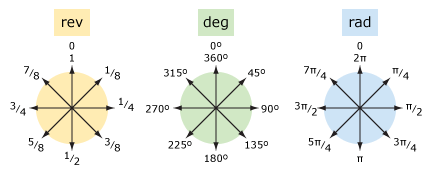
| szavak | rev | deg | rad |
|---|---|---|---|
| nem jövök | 0 | 0° | 0 |
| negyed fordulat | 1/4 | 90° | ⅲ /2 |
| fél fordulat | 1/2 | 180° | ⅲ |
| három-negyed fordulat | 3/4 | 270° | 3π/2 |
| teljes fordulat | 1 | 360° | 2π |
| tizenkettedik viszont | 1/12 | 30° | ⅲ /6 |
| nyolcadik kapcsold | 1/8 | 45° | ⅲ /4 |
| a hatodik viszont | 1/6 | 60° | ⅲ /3 |
| ötödik kapcsold | 1/5 | 72° | 2π/5 |
| harmadik kör | 1/3 | 120° | 2π/3 |
| két fordul | 2 | 720° | 4π |
| három fordul | 3 | 1080° | 6π |
átalakítani a forradalmak, hogy fokkal, szorozza 360. A fokról a fordulatszámra történő átváltáshoz ossza meg 360-mal.
fokok használatakor gyakran egész számokkal dolgozik, de amikor fordulatszámokat (vagy radiánokat) használ, gyakran törtekkel (vagy tizedesjegyekkel) dolgozik. A kézi számítások néha könnyebbek, ha forradalmakat használ, de néha könnyebbek, ha fokokat használ. Jó tudni mindkét utat.
a fordulat (fordulat) racionálisabb és természetesebb mértékegység, mint a fok. A szögek mélyebb megértését kapja, ha inkább a fordulatokra, mint a fokokra gondol. A szög alapvetően egy kör felosztása, nem pedig fokok összege. Például egy derékszög alapvetően egy kör negyede, nem pedig 90 fokos összeg.
osszuk fel a kört n egyenlő szektorra (lásd az alábbi ábrát). Az egyes szektorok szöge 1 / n rev = 360 / n 6-2 rad. Könnyebb megérteni ezt, ha inkább a fordulatokra gondol, mint a fokokra (vagy radiánokra).

nézzünk meg néhány alapvető geometriát fordulatszám és fok (és radián) felhasználásával. Az alábbi ábra kiegészítő szögeket, kiegészítő szögeket és háromszögeket mutat. A fogalmak világosabbak, ha inkább a fordulatokra, mint a fokokra gondolunk. Az aritmetika könnyebb lehet a fokok használatával, ha gondjai vannak a törtek összeadásával és kivonásával.
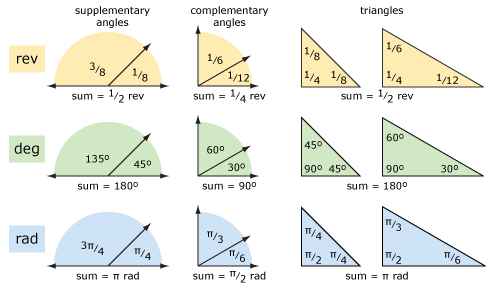
nézzük meg a sokszögeket (lásd az alábbi ábrát). Az n oldalú szabályos sokszög esetében a külső szög 1 / n Ford = 360 / n 6-2 rad. Könnyebb megérteni ezt, ha inkább a fordulatokra gondol, mint a fokokra (vagy radiánokra). A belső szög a külső szög kiegészítése.

forradalmak, fokozatok és Radiánok tanítása
szerintem jó lenne, ha a tanárok forradalmakat (fordulatokat) vezetnének be a fokozatok bevezetésével egy időben. Ez segít a diákoknak megérteni a szögeket egy alapvetőbb szinten, kevésbé függ a 360 tetszőleges mágikus számtól. A tanárok már bevezetni az általános fogalom, a fordulatszám (fordulat), amikor ilyeneket mondanak, hogy “egy teljes kör 360° – os”, de lehet, hogy a fogalom több számszerűen pontos azzal, hogy “egy teljes fordulatot, 360°, fél fordulj 180°, egy negyed fordulat 90° – os, illetve egy nyolcadik sor, 45° – os” vagy írás “1 rev = 360°, 1/2 rev = 180° – os, 1/4 rev = 90° – os, illetve 1/8 rev = 45°”. A hallgatóknak alkalmanként gyakorolniuk kell néhány számítást fordulat (fordulat) helyett fokokkal. Természetesen a hallgatóknak idejük nagy részét azzal kell tölteniük, hogy megtanulják számolni fokokkal (később pedig radiánokkal), mert ez a szabvány.
szögek trigonometria és kalkulus
végül vessünk egy gyors pillantást a fejlettebb matematika: trigonometria és kalkulus.
fontolóra vehetjük a trigonometrikus függvények (szinusz, koszinusz, érintő) fordulatainak használatát. Például ahelyett, hogy azt mondanánk, hogy cos(60 6) = 1/2 vagy cos(6/3) = 1/2 radiánokat használva, érdemes azt mondanunk, hogy cos(1/6) = 1/2 fordulatokat használva. De ez nem praktikus, mert a trigonometrikus függvények kiértékeléséhez számológépekre van szükség, és a számológépeknek általában csak DEG és RAD módjuk van, nem REV mód.
amikor a matematika mélyebb szintjeire megyünk, mint például a kalkulus és a matematikai analízis, kiderül, hogy a radiánok a legracionálisabb és legtermészetesebb egységek. Vegyük például ezt az alapvető egyenletet: a bűn(x)/x határa, amikor x megközelíti a 0-t, pontosan 1. Ez az egyenlet nem lenne olyan elegáns, ha a radiánoktól eltérő egységet használnánk.