How to make art with mathematics – Fractal Art-Senarius

Fractal art represents the alliance of art and mathematics. Tämä viimeaikainen taidemuoto käyttää tietokoneita tehdäkseen kuvia matemaattisista kaavoista. Fraktaalitaiteessa on usein geometrinen ulkonäkö, monimutkaisia kuvioita ja runsaasti yksityiskohtia. Mutta miten luodaan kuvia matemaattisista kaavoista ?

ensinnäkin, mitä ”fraktaali” tarkoittaa ?

tietojenkäsittelytieteilijä Benoit Mandelbrot löysi 1970-luvulla yhden tunnetuimmista fraktaalikuvista: Mandelbrotin joukon.

tämän löydön mahdollistaa tietokoneen kehittyminen erityisesti laskentatehon ansiosta. Se tapahtuu myös tieteellisessä yhteydessä kehityksen kaaosteoria, joka tutkii dynaamisia ilmiöitä (turbulenssi, vortices, fluid, värähtely, pilvi muoto, jne.).

samoin fraktaaligeometriaa esiintyy luonnon muodoissa, joissa on monimutkaisia ääriviivoja (lumihiutale, puun lehti, pilvien muoto, pyörremyrskyt, veriverkon arboresenssi, merenrantojen muoto jne.), että sitä oli vaikea ymmärtää ja mallintaa edellisten matemaattisten työkalujen avulla.

Fraktaalikuvien ominaisuudet

fraktaaliulottuvuus

termi ”fraktaali” viittaa ajatukseen ei-kokonaisesta, murtomittaisesta ulottuvuudesta. 1960-luvulle asti matematiikassa tutkittiin hajoavia kappaleita käyttäen kokonaislukumittoja:

A piste: dimension 0

a line: dimension 1

a plan: dimension 2

a volume: dimension 3

mutta kuvitelkaa paperiarkki. Se edustaa tasoa, joten sen ulottuvuus on yhtä suuri kuin 2. Jos me rutistaa tämä arkki, se nyt vie tilavuus (Ulottuvuus 3), mutta ei ole tilavuus, koska emme voi ”täyttää” rypistynyt arkki materiaalia kuin yksi täyttäisi säiliö. Rypistyneen arkin mitat ovat siis välillä 2-3: 2.568 esimerkiksi. Fraktaaliulottuvuus ! Fraktaaliesineillä on siis monimutkaisia, epäsäännöllisiä muotoja, joiden ääriviivat on taitettu ja taitettu itseensä.

itsensä samankaltaisuus

monimutkaisuudestaan huolimatta fraktaaliesineessä on samanlaisia yksityiskohtia. Zoomaus fraktaalin sisään näyttää saman yleiskaavan toistettuna eri asteikoilla ja äärettömyyteen. Osa muistuttaa siis kokonaisuutta. Tätä ominaisuutta kutsutaan asteikkovarianssiksi.

typologia

fraktaalit toistumisen mukaan

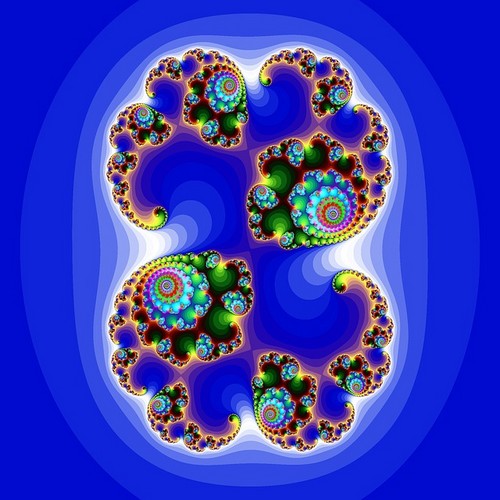
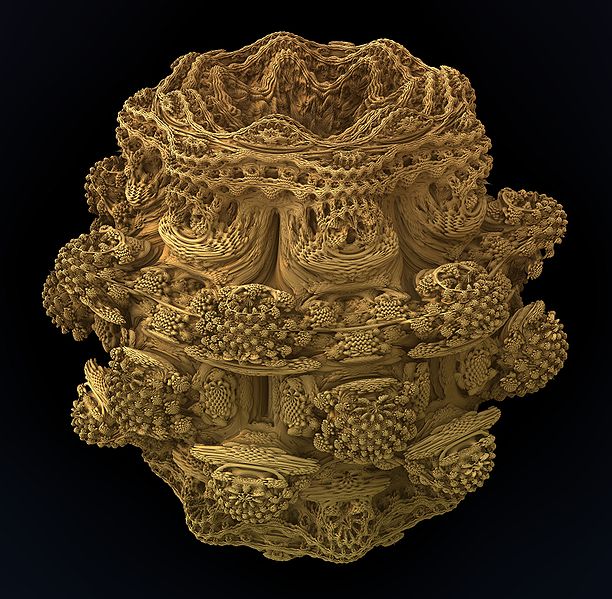
IFS, iteroidut funktiojärjestelmät

Fraktaalikuvien generointi,”yksinkertaisuus kasvattaa monimutkaisuutta”

fraktaalikuvien rakentaminen perustuu silmukassa toteutetun algoritmin käyttöön. Se on iteratiivinen prosessi, joka toistaa joukon yksinkertaisia operaatioita.

fraktaalit toistamalla

jokaisen avaruuden pisteen koordinaatit johdetaan yhtälöksi. Tulos syötetään sitten takaisin samaan yhtälöön. Operaatio suoritetaan useita kertoja peräkkäin (iteraatioita). Sitten testaamme tuloksen. Jos tulos pyrkii äärettömyyteen, lähtökohta ei ole kokonaisuudessa: se väritetään valkoiseksi. Jos tulos pysyy vakaana eli jaksollisena, niin lähtökohta on kokonaisuudessa: se väritetään mustaksi. Rajan pinnassa olevien pisteiden osalta on vaikeampi määrittää, ovatko ne joukolla vai sen ulkopuolella. Sen jälkeen on tarpeen tehdä lisää iteraatioita. Riippuen siitä, kuinka monta iterointia tarvitaan pisteen määrittämiseksi, se on värillinen eri sävyissä. Tämän rajan pisteet antavat fraktaalille sen monimutkaisen ja takkuisen ulkonäön.

Mandelbrotin joukon piirtämiseen käytetään kompleksilukuja, jotka kukin edustavat jotakin pikseliä tasossa. Suoritamme seuraavan yhtälön jokaiselle pisteelle: Zn + 1 = Zn2 + C, jossa Z0 = 0.

IFS, iteroidut funktiojärjestelmät

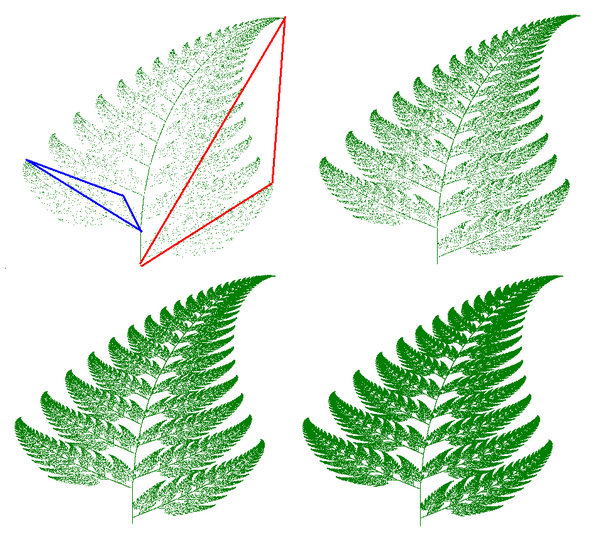
Kuvan konstruktio tehdään tässä itse kopioimalla. Mutta jokaisella kopiolla kopioitu kuva käy läpi geometrisen transformaation (lineaarinen transformaatio, jota matematiikassa edustaa lineaarinen funktio). Nämä muunnokset voivat olla rotaatioita, litistyksiä, leikkaamista … kopiot myös supistetaan ennen kuin ne sijoitetaan takaisin alkuperäiseen kuvaan. Prosessi toistetaan, kunnes muodostuu kuva.

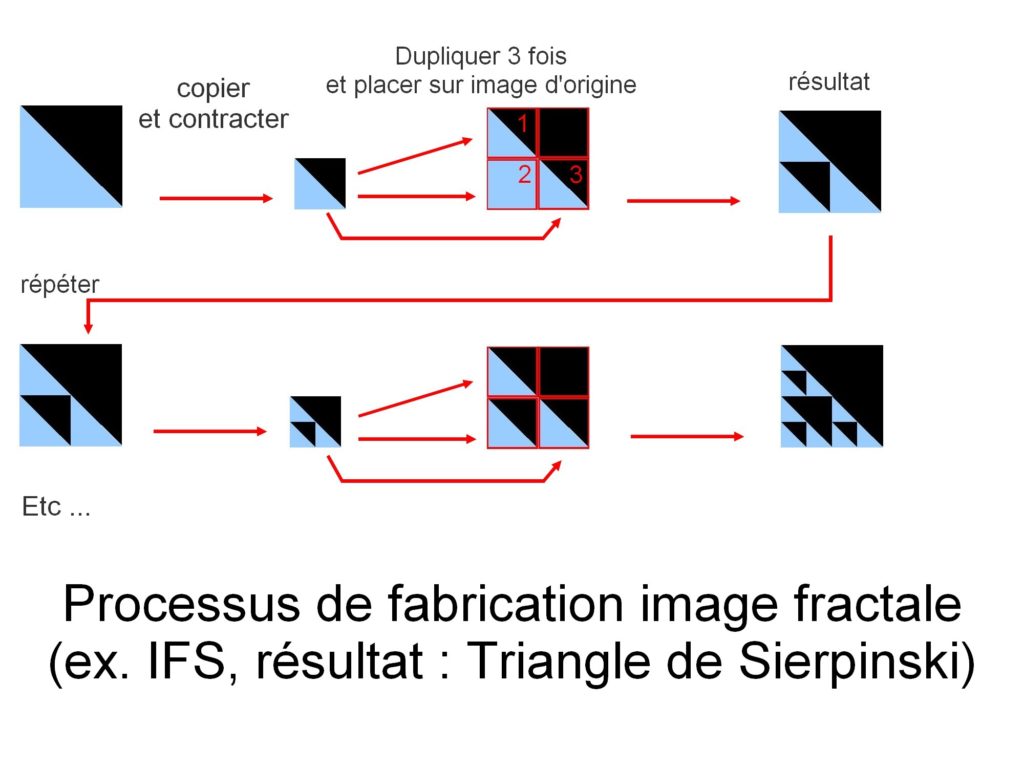
tästä esimerkistä saadaan kuva Sierpinskin kolmiosta.

toinen esimerkki on Kochin lumihiutalesukupolvi.

IFS voi helposti tuottaa kuvia, jotka muistuttavat luonnon kohteita, kuten puita, Saniaisia jne.