anovan taulukon laskeminen käsin Pythonilla
Tausta

varianssi-analyysi, josta käytetään tyypillisesti nimitystä ANOVA, on jotain, joka usein kaunistellaan johdantotilastoluokissa. Nykytekniikalla on helppo antaa tietokoneen tehdä kaikki laskelmat ja vain katsoa P-arvoa yllä olevan kaltaisen kiireisen näköisen taulukon päässä. Tässä artikkelissa käyn läpi, mitä nämä numerot ovat ja mitä ANOVA todella tekee.
anovan perusajatuksena on testata, onko otoksen alaryhmien välillä tilastollisesti merkitsevää eroa mitatuissa keskiarvoissa. Käsite juontaa juurensa noin 1920 Brittiläinen tilastotieteilijä Ronald Fisher, joka analysoi valtavia määriä tietoja sadon. Fisher todisti anovan avulla, että perunoiden keskipainossa oli merkittävä ero, kun käytettiin erilaisia lannoitteita.
havainnollistaakseni anovaa nykypäivänä tarkastelen ennemmin viinin hintoja kuin perunoiden painoja. Tämän esimerkin tiedot ovat Kaggle ’ s Wine Review-aineistosta, joka sisältää tuhansia arvosteluja viinipulloista. Olen suodattanut sen alas 3000 arvostelun osajoukkoon viineistä Yhdysvalloista, Italiasta ja Ranskasta (1000 per maa) ja käytän ANOVAA testatakseni, onko keskimääräisessä hinnassa tilastollisesti merkittävä ero alkuperämaiden välillä.
nopea juoni hintajakaumasta maittain näyttää kolme melko samanlaista jakoa, joissa suurin osa hinnoista on noin 25 dollaria pullolta.

kunkin maan keskiarvon perusteella voidaan todeta, että Ranskassa on keskimäärin kallein viini, seuraavana on Italia ja viimeisenä Yhdysvallat. Mutta kysymys kuuluu, onko kyseessä aito hintaero maiden välillä vai voisiko tämä johtua vain otosvaihtelusta? Tässä ANOVA astuu kuvaan.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
anovan neljä vaihetta ovat:
1. Muodostaa hypoteesin
2. Aseta merkitsevyystaso
3. Laske F-tilasto
4. F-statistin avulla saadaan p-arvo
5. Vertaa P-arvoa ja merkitsevyystasoa päättääksesi hylätäänkö nollahypoteesi
Muotoile hypoteesi
kuten lähes kaikissa tilastollisissa merkitsevyystesteissä, ANOVA aloittaa nollahypoteesin ja vaihtoehtoisen hypoteesin muodostamisella. Tämän esimerkin hypoteesit ovat seuraavat:
nollahypoteesi (H0): Viinin keskihinnassa ei ole eroa näiden kolmen maan välillä, ne ovat kaikki samanlaisia.
vaihtoehtoinen hypoteesi (H1): viinin keskihinta ei ole sama näiden kolmen maan välillä.
huomaa, että tämä on omnibus-testi, eli jos pystymme hylkäämään nollahypoteesin, se kertoo meille, että tilastollisesti merkittävä ero on jossain näiden maiden välillä, mutta se ei kerro, missä se on.
Aseta Merkitsevyystaso
merkitsevyystaso eli alfa on nollahypoteesimme hylkäämisen todennäköisyys, kun se todella pitää paikkansa. Toisin sanoen, se on todennäköisyys tehdä tyypin I virhe.
tyypillisesti pitäisi punnita tyypin I vs. tyypin II virheen tekemisen kustannuksia parhaan alfan määrittämiseksi kokeelle, mutta tässä leluesimerkissä aion vain käyttää standardia .05 meidän α-arvollemme.
lasketaan F-tilasto
F-tilasto on yksinkertaisesti otosten keskiarvojen välisen varianssin suhde otosten keskiarvojen sisällä olevaan varianssiin. Tätä ANOVA-testiä varten tarkastelemme, kuinka kaukana kunkin maan keskimääräinen viinin hinta on yleisestä keskihinnasta ja jakamalla se sillä, kuinka paljon vaihtelua hinnassa on kunkin maan otosjakaumassa. Alla on F-statistiikan kaava, joka voi näyttää monimutkaiselta, kunnes hajotamme sen.
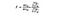
SSB = ryhmien välisten neliöiden summa. Tämä on yhteenlasku kunkin ryhmän keskiarvon ja kokonaiskeskiarvon välisestä potenssierosta, joka on kerrottuna alkioiden lukumäärällä ryhmää kohti. Tässä esimerkissä otamme kunkin maan viinihinnan keskiarvon, vähennämme sen kokonaiskeskiarvosta, neliöimme erotuksen ja kerromme 1000: lla (datapisteiden määrä maata kohti).
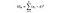
SSW = neliöiden summa ryhmien sisällä. Tämä on ryhmän keskiarvon ja kunkin ryhmän arvon neliöllisen erotuksen yhteenlasku. Ranskalle ottaisimme ranskalaisen viinin keskihinnan, sitten vähentäisimme ja neliöisimme kunkin ranskalaisen viinipullon erotuksen kyseisen ryhmän tuhannesta datapisteestä.
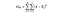
DoFB = ryhmien väliset vapausasteet, yksinkertaisesti ryhmien lukumäärä miinus 1. Vertailemme kolmea eri maata, joten vapausasteet ovat tässä 2.
DoFW = vapausasteet ryhmien sisällä, yksinkertaisesti datapisteiden lukumäärä miinus ryhmien lukumäärä. Meillä on 3 000 datapistettä ja kolme eri maata, joten tämä on 2 997 tässä esimerkissä.
jakamalla ryhmän neliöiden summa sen vapausasteilla saadaan kyseisen ryhmän keskimääräiset neliöt, ja F-statistiikka on vain niiden neliöiden keskineliöiden suhde, jotka ovat keskiarvon sisällä olevien neliöiden välillä.
alle I laskee käsin nämä arvot Pythonissa ja päätyy F-Statistiikkaan ~4,07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
F-statistiikan avulla lasketaan p-arvo
kun meillä on F-statistiikka, kytkemme sen F-jakaumaan saadaksemme p-arvon. Voit löytää taulukon näille arvoille minkä tahansa tilastokirjan takaa tai on paljon helpompia online-laskimia, jotka tekevät tämän puolestasi. Kun meillä on tietyt vapausasteet, F-tilasto 4,07 antaa p-arvon .0172.

vertaa P-arvoa ja merkitsevyystasoa päättääksemme, hylätäänkö nollahypoteesi
p-arvomme tarkoittaa, että olettaen nollahypoteesin (kaikissa maissa on sama viinin keskihinta) olevan totta, on suurin piirtein 1.7% mahdollisuus nähdä tiedot, jotka meillä on pelkällä näytteenottotodennäköisyydellä. Asettamalla merkityksellisyystasomme eli alfamme 5% : iin ennen kaikkea tätä, totesimme olevamme valmiita hyväksymään 5%: n mahdollisuuden hylätä nolla, kun se on totta. Koska p-arvomme on alle ennalta määritetyn merkitsevyystasomme, voimme hylätä nollahypoteesin ja sanoa, että viinin keskihinnassa on tilastollisesti merkittävä ero maiden välillä.
muista, että ANOVA on omnibus-testi, eli koska pystymme hylkäämään nollan, tiedämme, että viinien keskihinnoissa on eroja maiden välillä, mutta ei tarkalleen missä. Jotta löytäisimme, missä ero on, tekisimme hypoteesitestejä kahden maan välillä kerrallaan.
Automatic ANOVA
kuten useimmat asiat elämässä, Pythonilla on intuitiivinen ratkaisu anovan johtamiseen statsmodel-kirjastolla. Alla oleva koodi tekee kaikki tässä artikkelissa esitetyt laskelmat ja tuottaa yhteenvetotaulukon, jossa on F-tilasto ja p-arvo.

Kiitos lukemisesta, koko koodi ja tiedot löytyvät GitHub-sivultani.