Which is the best unit of measure for angles-revolutions, degrees, or radians?
kierrokset
opimme harvoin käyttämään geometrisille kulmille yksinkertaisinta, luonnollisinta mittayksikköä, vallankumousta (rev). Muita nimiä tälle yksikölle ovat täysi ympyrä, turn, full turn ja rotation (rot). Nämä kaikki ovat hyviä nimiä ja tarkoittavat samaa asiaa.
1 täysi kierros = 1 kierros = 1 kierros = 1 kierros = 360°
asteet
peruskoulussa opimme, että kulmat mitataan asteina (°).
1 täysi ympyrä = 360°
Radiaanit
lukion trigonometrian ja laskennan tunneilla opimme, että matemaatikot suosivat radiaaneja (rad).
1 täysi ympyrä = 2π rad
Huomaa: Jos et ole vielä koulussa oppinut radiaaneista, voit jättää radiaanit huomiotta kaikessa alla olevassa.
verrataan kierroslukuja, asteita ja radiaaneja
verrataan kierroslukuja ja asteita (ja radiaaneja).
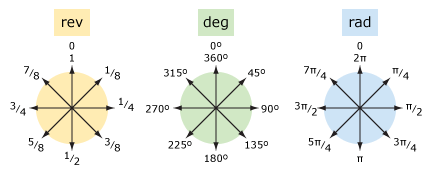
| sanat | rev | deg | rad |
|---|---|---|---|
| ei käännöstä | 0 | 0° | 0 |
| neljänneskierros | 1/4 | 90° | π/2 |
| puolivääntö | 1/2 | 180° | π |
| kolmen vartin kierros | 3/4 | 270° | 3π/2 |
| täysi kierros | 1 | 360° | 2π |
| kahdestoista vuoro | 1/12 | 30° | π/6 |
| kahdeksas kierros | 1/8 | 45° | π/4 |
| kuudes vuoro | 1/6 | 60° | π/3 |
| viides käännös | 1/5 | 72° | 2π/5 |
| kolmas kierros | 1/3 | 120° | 2π/3 |
| kaksi kierrosta | 2 | 720° | 4π |
| kolme kierrosta | 3 | 1080° | 6π |
muunnetaan kierroksista asteiksi, kerrotaan 360: llä. Jos haluat muuntaa asteista kierroksiin, Jaa 360: llä.
asteita käytettäessä käytetään usein kokonaislukuja, mutta kierroksia (tai radiaaneja) käytettäessä käytetään usein murtolukuja (tai desimaaleja). Käsin laskeminen on joskus helpompaa, kun käytät kierroksia, mutta joskus helpompaa, kun käytät astetta. On hyvä tietää molempiin suuntiin.
kierrokset (kierrokset) ovat astetta rationaalisempi ja luonnollisempi mittayksikkö. Saat syvemmän käsityksen kulmista, jos ajattelet vallankumouksia asteiden sijaan. Kulma on perusteellisemmin osa-alue, ympyrän sijaan summa astetta. Esimerkiksi suora kulma on perusteellisemmin ympyrän neljäsosa eikä 90 asteen summa.
jaetaan ympyrä n: n tasasektoreihin (katso alla oleva kaavio). Kunkin sektorin kulma on 1/n rev = 360/n° = 2π / n rad. Tämä on helpompi ymmärtää, jos ajattelee kierroslukuja eikä asteita (tai radiaaneja).

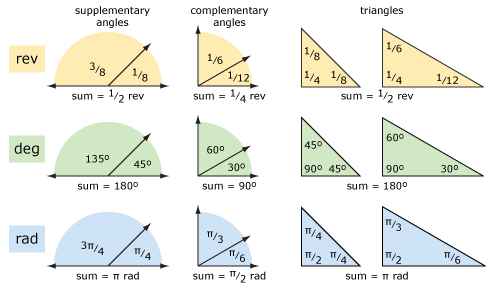
Katsotaanpa joitakin perus geometria käyttäen kierrosta ja astetta (ja radiaanit). Alla olevassa kaaviossa esitetään täydentäviä kulmia, täydentäviä kulmia ja kolmioita. Käsitteet ovat selkeämpiä, jos ajattelee vallankumouksia asteiden sijaan. Aritmeettinen voi olla helpompaa käyttämällä astetta, jos sinulla on vaikeuksia lisätä ja vähentää jakeet.
Katsotaanpa polygoneja (katso kaavio alla). Säännöllisessä monikulmiossa, jossa on n-sivut, ulkokulma on 1/n rev = 360/n° = 2π/n rad. Tämä on helpompi ymmärtää, jos ajattelee kierroslukuja eikä asteita (tai radiaaneja). Sisäkulma on ulkokulman täydennys.

opetuksessa vallankumoukset, tutkinnot ja Radiaanit
mielestäni olisi hyvä, jos opettajat ottaisivat kierrokset (kierrokset) käyttöön samaan aikaan, kun he ottavat tutkinnot käyttöön. Tämä auttaa oppilaita ymmärtämään näkökulmia perustasolla, vähemmän riippuvainen mielivaltaisesta taikaluvusta 360. Opettajat esittelevät jo yleiskäsitteen kierroksista (kierroksista), kun he sanovat asioita kuten ”täysi ympyrä on 360°”, mutta he voivat tehdä käsitteestä numeerisesti tarkemman sanomalla ”täysi kierros on 360°, puoli kierrosta on 180°, neljäs kierros on 90° ja kahdeksas kierros on 45°” tai kirjoittamalla ”1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90° ja 1/8 rev = 45°”. Opiskelijoiden tulisi joskus harjoitella tehdä muutamia laskelmia käyttäen kierroksia (kierrosta) eikä astetta. Tietenkin, opiskelijoiden täytyy viettää suurimman osan ajastaan oppia laskemaan kanssa astetta (ja myöhemmin, radiaanit), koska se on standardi.
kulmat Trigonometriassa ja Calculus
lopuksi, katsotaanpa nopeasti kehittyneempää matematiikkaa: trigonometriaa ja calculus.
voidaan harkita kierrosta, jossa on trigonometriset funktiot (sini, kosini, tangentti). Esimerkiksi sen sijaan, että sanoisimme cos(60°) = 1/2 tai cos(π/3) = 1/2 käyttäen radiaaneja, voisimme sanoa cos (1/6) = 1/2 käyttäen kierroksia. Tämä ei kuitenkaan ole käytännöllistä, koska trigonometristen funktioiden arvioimiseen tarvitaan laskimia, ja laskimissa on tyypillisesti vain DEG-ja RAD-tiloja, ei REV-tilaa.
kun mennään matematiikan syvemmille tasoille, kuten laskemiseen ja matemaattiseen analyysiin, käy ilmi, että radiaanit ovat rationaalisimpia ja luonnollisimpia yksiköitä. Ajatellaanpa esimerkiksi tätä perusyhtälöä: sinin(x)/x: n raja x: n lähestyessä 0 on tasan 1. Yhtälö ei olisi niin tyylikäs, jos käyttäisimme mitä tahansa muuta yksikköä kuin radiaaneja.