hvilken er den bedste måleenhed for vinkler-omdrejninger, grader eller radianer?
omdrejninger
vi lærer sjældent at bruge den enkleste, mest naturlige måleenhed for geometriske vinkler, revolutionen (rev). Andre navne på denne enhed er fuld cirkel, drejning, fuld drejning og rotation (rot). Disse er alle gode navne, og de betyder alle det samme.
1 fuld cirkel = 1 omdrejning = 1 rot = 360°
grader
i grundskolen lærer vi, at vinkler måles i grader (liter).
1 fuld cirkel = 360°
radianer
i high school trigonometri og calculus klasser lærer vi, at matematikere foretrækker radianer (rad).
1 fuld cirkel = 2 liter rad
Bemærk: Hvis du endnu ikke har lært om radianer i skolen, kan du ignorere radianerne i alt nedenfor.
sammenligning af omdrejninger, grader og radianer
lad os sammenligne omdrejninger og grader (og radianer).
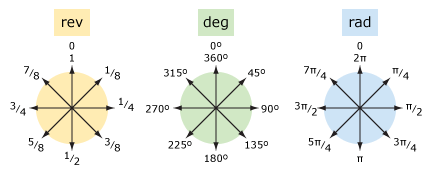
| ord | rev | gr | rad |
|---|---|---|---|
| ingen tænder | 0 | 0° | 0 |
| kvart omgang | 1/4 | 90° | π/2 |
| halv omgang | 1/2 | 180° | π |
| tre-kvart omgang | 3/4 | 270° | 3π/2 |
| fuld sving | 1 | 360° | 2π |
| tolvte igen | 1/12 | 30° | π/6 |
| ottende igen | 1/8 | 45° | π/4 |
| sjette igen | 1/6 | 60° | π/3 |
| femte tur | 1/5 | 72° | 2π/5 |
| tredje tur | 1/3 | 120° | 2π/3 |
| to omgange | 2 | 720° | 4π |
| tre omgange | 3 | 1080° | 6π |
for At konvertere fra omdrejninger til grader, skal du gange med 360. For at konvertere fra grader til omdrejninger, divider med 360.
når du bruger grader, arbejder du ofte med heltal, men når du bruger omdrejninger (eller radianer), arbejder du ofte med brøker (eller decimaler). Håndberegninger er undertiden lettere, når du bruger omdrejninger, men nogle gange lettere, når du bruger grader. Det er godt at kende begge veje.
omdrejninger (sving) er en mere rationel og naturlig måleenhed end grader. Du får en dybere forståelse af vinkler, hvis du tænker på revolutioner snarere end grader. En vinkel er mere fundamentalt en underinddeling af en cirkel snarere end en sum af grader. For eksempel er en ret vinkel mere fundamentalt en fjerdedel af en cirkel snarere end en sum på 90 grader.
lad os opdele cirklen i n lige sektorer (se diagram nedenfor). Vinklen for hver sektor er 1/n rev = 360/n liter = 2 liter/n rad. Det er lettere at forstå dette, hvis du tænker på omdrejninger snarere end grader (eller radianer).

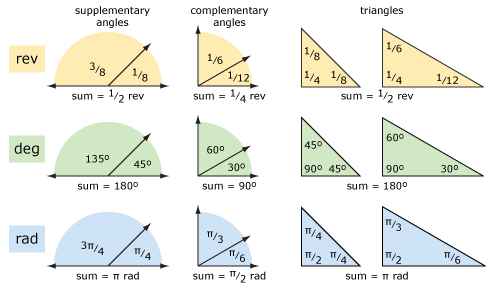
lad os se på nogle grundlæggende geometri ved hjælp af omdrejninger og grader (og radianer). Diagrammet nedenfor viser supplerende vinkler, komplementære vinkler og trekanter. Begreberne er klarere, hvis du tænker på revolutioner snarere end grader. Det aritmetiske kan være lettere at bruge grader, hvis du har problemer med at tilføje og subtrahere fraktioner.
lad os se på polygoner (se diagram nedenfor). For en regelmæssig polygon med n-sider er den udvendige vinkel 1/n rev = 360/n liter = 2 liter/n rad. Det er lettere at forstå dette, hvis du tænker på omdrejninger snarere end grader (eller radianer). Den indvendige vinkel er tillægget til den udvendige vinkel.

undervisning revolutioner, grader, og radianer
jeg tror, det ville være godt, hvis lærerne ville indføre revolutioner (sving) på samme tid, at de indfører grader. Dette vil hjælpe eleverne til at forstå vinkler på et mere grundlæggende niveau, mindre afhængig af det vilkårlige magiske nummer 360. Lærere, der allerede indføre det generelle koncept om revolutioner (vender sig), når de siger ting som “en fuld cirkel er 360°”, men de kan gøre konceptet mere præcis numerisk ved at sige “fuld sving 360°, en halv omgang, er 180°, en kvart omdrejning er 90°, og en ottende igen er 45°” eller ved at skrive “1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90°, og 1/8 rev = 45°”. Studerende bør lejlighedsvis øve sig på at lave et par beregninger ved hjælp af omdrejninger (sving) snarere end grader. Selvfølgelig skal eleverne bruge det meste af deres tid på at lære at beregne med grader (og senere radianer), fordi det er standarden.
vinkler i trigonometri og Calculus
endelig, lad os tage et hurtigt kig på mere avanceret matematik: trigonometri og calculus.
vi kan overveje at bruge omdrejninger med trigonometriske funktioner (sinus, cosinus, tangent). For eksempel, i stedet for at sige cos(60 list) = 1/2 eller cos(list/3) = 1/2 ved hjælp af radianer, vil vi måske sige cos(1/6) = 1/2 ved hjælp af omdrejninger. Men dette er ikke praktisk, fordi vi er afhængige af regnemaskiner for at evaluere de trigonometriske funktioner, og regnemaskiner har typisk kun deg-og RAD-tilstande, ikke REV-tilstand.
når vi går til dybere niveauer af matematik, såsom beregning og matematisk analyse, viser det sig, at radianer er de mest rationelle og naturlige enheder. Overvej for eksempel denne grundlæggende ligning: grænsen for synd(s)/s som nærmer sig 0 er nøjagtigt 1. Denne ligning ville ikke være så elegant, hvis vi brugte en anden enhed end radianer.