fraktal kunst repræsenterer alliancen mellem kunst og matematik. Denne nylige kunstform bruger computere til at lave billeder fra matematiske formler. Fraktal kunst har et ofte geometrisk udseende, indviklede mønstre og et væld af detaljer. Men hvordan kan du gå om at skabe billeder fra matematiske formler ?
først og fremmest, hvad betyder “fraktal”?
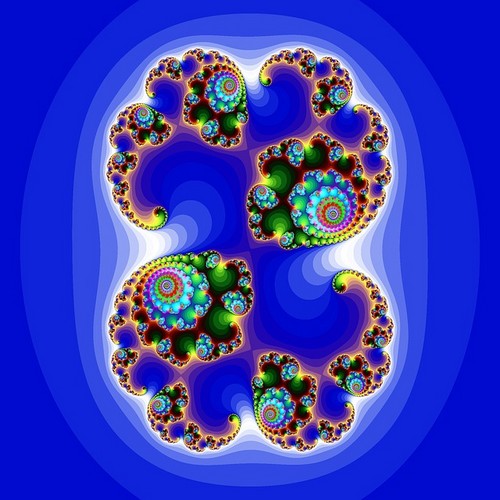
i 1970 ‘ erne opdagede computerforsker Benoit Mandelbrot et af de mest berømte fraktalbilleder: Mandelbrot-sættet.

denne opdagelse er muliggjort af udviklingen af computer, især takket være computerkraften. Det finder også sted i den videnskabelige sammenhæng med udviklingen af kaosteorien, der studerer dynamiske fænomener (turbulens, hvirvler i en væske, svingning, skyform osv.).
ligeledes findes fraktalgeometri i naturens former med komplekse konturer (snefnug, træblad, form af skyer, hvirvler, arborescens af blodnetværket, form af maritime kyster osv.) at det var svært at forstå, og at modellere med de tidligere matematiske værktøjer.

Karakteristik af fraktale billeder
den fraktale dimension
udtrykket “fraktal” henviser til ideen om en ikke-hel, fraktioneret dimension. Indtil 1960 ‘ erne studerede matematik nedbrydelige objekter ved hjælp af heltalsdimensioner:
et punkt: dimension 0
en linje: dimension 1
en plan: dimension 2
et volumen: dimension 3
men forestil dig et ark papir. Det repræsenterer et plan, har derfor en dimension svarende til 2. Hvis vi smuldrer dette ark, optager det nu et volumen (dimension 3), men er ikke et volumen, fordi vi ikke kan “fylde” det krøllede ark med et materiale, som man ville fylde en beholder. Dimensionen af det krøllede ark er derfor mellem 2 og 3 : 2.568 for eksempel. En fraktal dimension ! Fraktale objekter har således komplekse, uregelmæssige former med konturer foldet og foldet ind på sig selv.
Selvlighed
på trods af dets kompleksitet udviser et fraktalt objekt lignende detaljer. En fraktal viser det samme samlede mønster gentaget i forskellige skalaer og ind i uendelig. En del svarer derfor til helheden. Denne egenskab kaldes skala invariance.

typologi
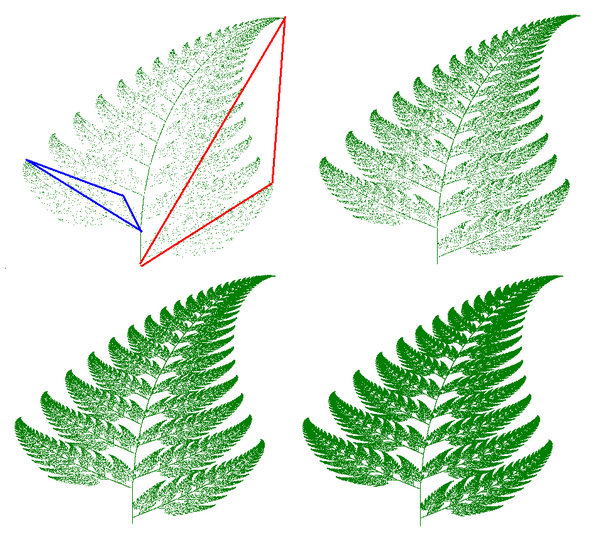
fraktaler ved gentagelse

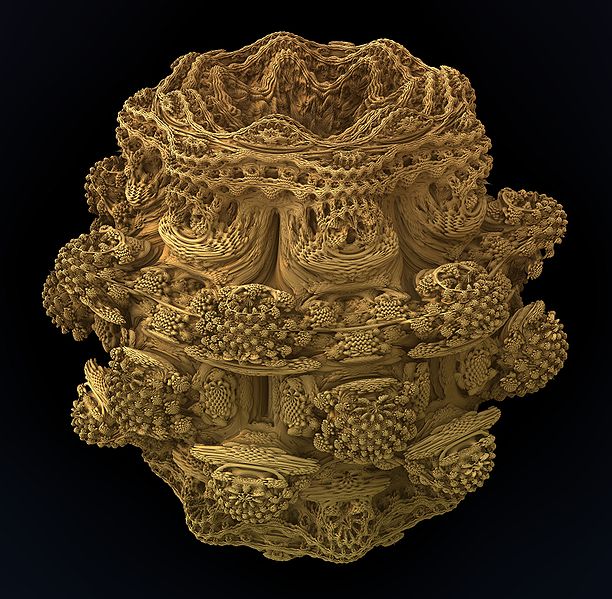
IFS, itererede funktioner systemer



Generation af fraktale billeder, “enkelhed racer kompleksitet”
konstruktionen af fraktale billeder er baseret på brugen af algoritme udført i en løkke. Det er en iterativ proces, der gentager en række enkle operationer.
fraktaler ved gentagelse
for hvert punkt i rummet føres koordinaterne for punktet ind i en ligning. Resultatet føres derefter tilbage i den samme ligning. Operationen udføres flere gange i træk (iterationer). Så tester vi resultatet. Hvis resultatet har tendens til uendelig, er udgangspunktet ikke i det hele : det er farvet hvidt. Hvis resultatet forbliver stabilt eller periodisk, er udgangspunktet i det hele : det er farvet sort. For punkter på grænsen er det vanskeligere at afgøre, om de er i sættet eller udenfor. Det er derefter nødvendigt at udføre flere iterationer. Afhængigt af antallet af iterationer, der kræves for at bestemme punktet, er det farvet i forskellige nuancer. Punkterne i denne grænse giver fraktalen sit komplicerede og sammenfiltrede udseende.
for at tegne Mandelbrot-sættet bruger vi komplekse tal, der hver repræsenterer et punkt på flyet. Vi udfører følgende ligning for hvert punkt : SN + 1 = SN2 + C, med S0 = 0.
IFS, iterated functions systems
billedkonstruktion udføres her ved at kopiere sig selv. Men med hver kopi gennemgår det kopierede billede en geometrisk transformation (en lineær transformation repræsenteret i matematik ved en lineær funktion). Disse transformationer kan være rotationer, udfladning, klipning … kopierne er også kontraheret, før de placeres tilbage på det originale billede. Processen gentages, indtil et billede er dannet.
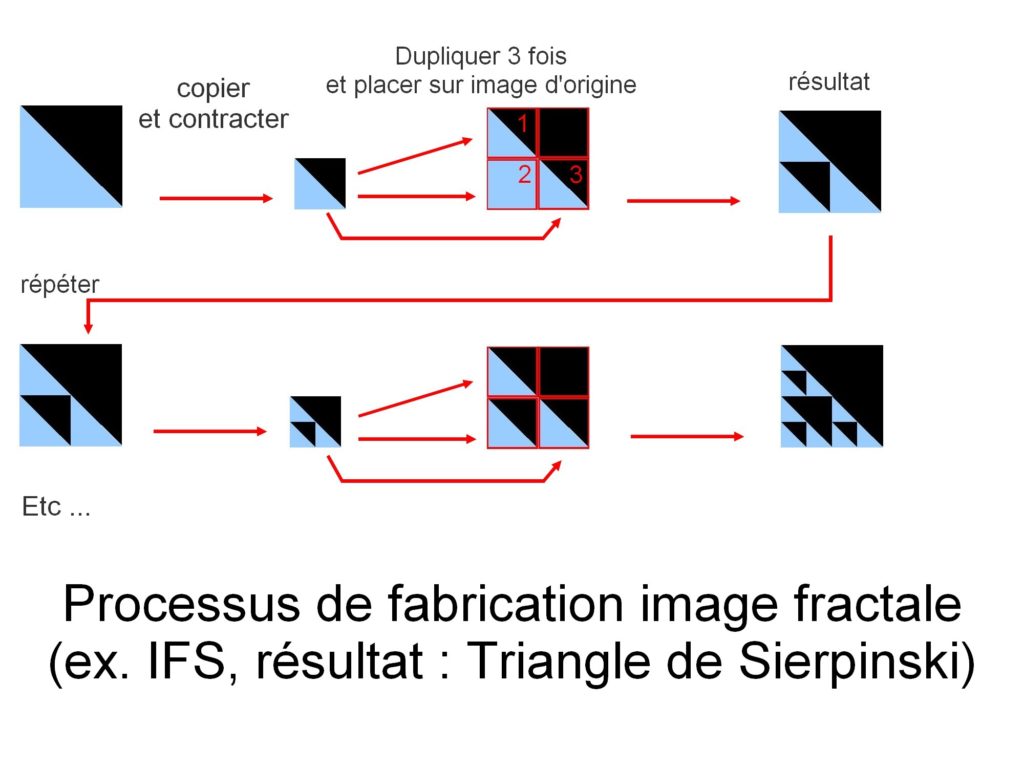
dette eksempel resulterer i billedet af Sierpinski-trekanten.
et andet eksempel er generationen af Koch snefnug.

IFS kan nemt producere billeder, der minder om naturlige genstande, såsom træer, bregner osv.