manuel beregning af en ANOVA-tabel med Python
baggrund

variansanalyse, typisk omtalt som ANOVA, er noget, der ofte glanses over i indledende statistikklasser. Med dagens teknologi er det nemt at lade computeren udføre alle beregningerne og bare se på p-værdien i slutningen af et travlt bord som den ovenfor. I denne artikel vil jeg gennemgå, hvad disse tal er, og hvad ANOVA faktisk gør.
hovedideen bag ANOVA er at teste, om der er en statistisk signifikant forskel i A det målte middel mellem undergrupper af en prøve. Konceptet går tilbage til omkring 1920 med en britisk statistiker ved navn Ronald Fisher, der analyserede enorme mængder data om afgrødeudbytter. Fisher brugte ANOVA til at bevise, at der var en betydelig forskel i gennemsnitsvægten af kartofler, når forskellige gødninger blev brugt.
for at demonstrere ANOVA i dag vil jeg se på priserne på vin snarere end vægten af kartofler. Dataene for dette eksempel er fra Kaggles vinanmeldelsesdatasæt, som indeholder tusindvis af anmeldelser på flasker vin fra Vinentusiast. Jeg har filtreret det ned til en delmængde på 3.000 anmeldelser for vine fra USA, Italien og Frankrig (1.000 pr.land) og vil bruge ANOVA til at teste, om der er en statistisk signifikant forskel i gennemsnitsprisen mellem oprindelseslandene.
et hurtigt plot af prisfordelingen efter land viser tre temmelig lignende distributioner, med de fleste priser omkring $25 En flaske.

når vi tager gennemsnittet af hvert land, ser vi, at Frankrig i gennemsnit har den dyreste vin efterfulgt af Italien og derefter endelig USA. Men spørgsmålet er, er dette en reel prisforskel mellem lande, eller kan det bare skyldes stikprøvevariation? Det er her ANOVA kommer i spil.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
de fire trin til ANOVA er:
1. Formulere en hypotese
2. Indstil et signifikansniveau
3. Beregn en F-statistik
4. Brug f-statistikken til at udlede en p-værdi
5. Sammenlign p-værdien og signifikansniveauet for at afgøre, om nulhypotesen skal afvises
formuler en hypoteser
som med næsten alle statistiske signifikanstest starter ANOVA med at formulere en null-og alternativ hypotese. For dette eksempel er hypoteserne som følger:
Nulhypotese (H0): Der er ingen forskel i gennemsnitsprisen på vin mellem de tre lande; de er alle de samme.
alternativ hypotese (H1): gennemsnitsprisen på vin er ikke den samme mellem de tre lande.
Bemærk, Dette er en omnibus-test, hvilket betyder, at hvis vi er i stand til at afvise nulhypotesen, vil det fortælle os, at der findes en statistisk signifikant forskel et sted mellem disse lande, men det vil ikke fortælle os, hvor det er.
Indstil et signifikansniveau
signifikansniveauet, eller alfa, er sandsynligheden for at afvise vores nulhypotese, når det faktisk gælder. Med andre ord er det sandsynligheden for at lave en type i-fejl.
typisk skal man afveje omkostningerne ved at lave en type I vs. en Type II-fejl for at bestemme den bedste alfa til et eksperiment, men for dette legetøjseksempel vil jeg bare bruge standarden .05 for vores KP værdi.
Beregn en F-statistik
F-statistikken er simpelthen et forhold mellem variansen mellem prøver betyder til variansen inden for prøveorganer. Til denne ANOVA-test vil vi se på, hvor langt hvert lands gennemsnitlige vinpris er fra den samlede gennemsnitspris, og dividere det med hvor meget variation i pris der er inden for hvert lands prøvefordeling. F-statistikformlen er under, hvilket kan se kompliceret ud, indtil vi nedbryder det.
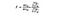
SSB = summen af kvadrater mellem grupper. Dette er summen af den kvadratiske forskel mellem hver gruppes gennemsnit og det samlede gennemsnit gange antallet af elementer pr. I dette eksempel tager vi gennemsnittet af hvert lands vinpris, trækker det fra det samlede gennemsnit, kvadrerer forskellen og multiplicerer med 1.000 (antallet af datapunkter pr.
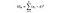
SV = summen af kvadrater inden for grupper. Dette er summen af den kvadratiske forskel mellem gruppegennemsnittet og hver værdi i gruppen. For Frankrig ville vi tage gennemsnitsprisen på fransk vin og derefter trække og kvadrere forskellen for hver flaske fransk vin af de tusind datapunkter i denne gruppe.
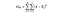
DoFB = frihedsgrader mellem grupper, simpelthen antallet af grupper minus 1. Vi har tre forskellige lande, vi sammenligner, så frihedsgraderne her er 2.
DOF = frihedsgrader inden for grupper, simpelthen antallet af datapunkter minus antallet af grupper. Vi har 3.000 datapunkter og tre forskellige lande, så dette er 2.997 for dette eksempel.
at dividere summen af kvadrater for en gruppe med dens frihedsgrader giver middelkvadraterne for den gruppe, og f-statistikken er kun et forhold mellem middelkvadraterne mellem over middelkvadraterne inden for.
nedenfor beregner jeg manuelt disse værdier i Python og ender med en F-statistik på ~4.07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
brug F-statistikken til at beregne en p-værdi
når vi har vores F-statistik, sætter vi den i en F-distribution for at få en p-værdi. Du kan finde en tabel for disse værdier på bagsiden af enhver statistikbog, eller der er langt lettere online regnemaskiner, der gør dette for dig. Med vores specifikke frihedsgrader giver en F-statistik på 4,07 en p-værdi .0172.

Sammenlign p-værdien og signifikansniveauet for at afgøre, om nulhypotesen skal afvises
vores p-værdi betyder, at hvis man antager nulhypotesen (alle lande har samme gennemsnitspris på vin) er sandt, er der omtrent en 1.7% chance for at se de data, vi har ved ren prøveudtagning chance. Ved at sætte vores signifikansniveau, eller alfa, på 5% før alt dette, sagde vi, at vi ville være villige til at acceptere en 5% chance for at afvise null, når det er sandt. Da vores p-værdi ligger under vores forudbestemte signifikansniveau, kan vi afvise nulhypotesen og sige, at der er en statistisk signifikant forskel i gennemsnitsprisen på vin mellem lande.
Husk, at ANOVA er en omnibus-test, hvilket betyder, Fordi vi er i stand til at afvise null vi ved, at der findes en forskel mellem de gennemsnitlige vinpriser mellem lande, men ikke nøjagtigt hvor. For at finde ud af, hvor forskellen ligger, ville vi derefter gennemføre hypotesetest mellem to lande ad gangen.
automatisk ANOVA
ligesom med de fleste ting i livet har Python en intuitiv løsning til at udføre ANOVA med statsmodel-biblioteket. Nedenstående kode udfører alle beregningerne i denne artikel og udsender en oversigtstabel komplet med en F-statistik og p-værdi.

tak for læsning, fuld kode og data kan findes på min GitHub side.