Jak vytvořit křivku zvonu v Tabulkách Google?

zvonová křivka je užitečný graf pro porovnání porovnání datových bodů se zbytkem dat.

jsem si jist, že jste slyšeli o lidech, kteří mluví o získání hodnocení na základě zvonové křivky.

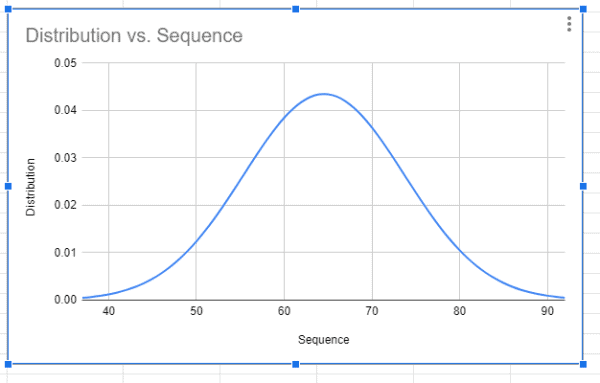
tento graf pomáhá ukázat, kde většina datových bodů existuje v grafu, jak blízko jsou tyto datové body k sobě a které datové body jsou považovány za odlehlé hodnoty.

tento tutoriál ukazuje, jak vytvořit graf bell curve v Tabulkách Google z existující datové sady.

zatímco listy má nepřeberné množství vestavěných grafů nástrojů, budete muset spustit několik výpočtů generovat křivku zvonu.

jak vytvořit křivku zvonu v Tabulkách Google

grafy křivky Zvonu mají tendenci nejlépe pracovat s datovými body, které jsou obecně blíže průměru než ve srovnání s extrémy.

v našem příkladu budeme pracovat s hypotetickým seznamem 50 hodnocení automobilů.

než budeme moci sestavit náš graf, musíme provést několik výpočtů:

1. Průměrná (střední) hodnota.
2. hodnota směrodatné odchylky (buď jako populace, nebo jako vzorek).
3. hodnoty směrodatné odchylky + / – 3 průměru.
4. rozsah sekvence.
5. normální rozdělení pro všechny datové body.

než začnete, vytvořte řadu pomocných sloupců pro výpočty, které budete potřebovat k vytvoření grafu.

v příkladu jsem přidal následující sloupce:

1. C: sekvence
2. D: distribuce
3. E: průměr
4. F: směrodatná odchylka
5. G: nízká
6. H: vysoká

postupujte takto a vytvořte graf křivky zvonu v Tabulkách Google:

1. vypočítejte průměrnou hodnotu dat, která vytváříte zvonovou křivku, pro použití průměrné funkce. V příkladu jsem použil vzorec =Average (B2: B51) v buňce E2.
2. průměrné výnosy jako 64.54 v příkladu.
3. Určete směrodatnou odchylku pomocí vzorce =STV.P () Pokud pracujete se všemi čísly v populaci nebo =STV.S () pokud pracujete se vzorkem dat. Příklad používá vzorec =STDEV.S (B1: B51) v buňce F2, protože je to jen vzorek dostupných vozů.
4. směrodatná odchylka se v příkladu vrací jako 9.1767.
5. Vypočítejte nízkou hodnotu směrodatné odchylky průměru pomocí tohoto vzorce: = průměr-3 * směrodatná odchylka odkazem na odpovídající buňky. V příkladu jsem použil vzorec =E2-3 * F2 v buňce G2.
6. příklad vrací hodnotu 37.0098
7. Vypočítejte vysokou směrodatnou odchylku průměru pomocí tohoto vzorce: = průměr+3 * směrodatná odchylka odkazem na odpovídající buňky. V příkladu jsem použil vzorec =E2+3 * F2 v buňce H2.
8. příklad vrací hodnotu 92.07
9. Vygenerujte posloupnost čísel ve sloupci sekvence pomocí následujícího vzorce: =sekvence (Vysoká-Nízká+1,1, nízká). V příkladu jsem použil vzorec: = sekvence (H2-G2+1,1, G2)v buňce C2. Tím se vrátí posloupnost celých čísel v rozsahu grafu.
10. dále Vypočítejte normální rozdělení všech datových hodnot pomocí normy.DIST vzorec pomocí tohoto vzoru: =ArrayFormula(NORM.DIST (rozsah datových buněk, průměr, směrodatná odchylka, false)). V příkladu jsem použil: = ArrayFormula (NORM.DIST(C2: C57,$E $ 2,$F $ 2, false)) v buňce D2.
11. vrátí distribuční hodnoty pro všechny skóre.
12. nyní je konečně čas sestavit graf. Chcete-li začít, vyberte všechny hodnoty ve sloupcích „sekvence“ a „distribuce“.
13. otevřete rozbalovací nabídku “ Vložit „z záhlaví a vyberte“ graf.“
14. v editoru grafu vyberte „hladký graf“ v části „Typ grafu“ na kartě „Nastavení“.
15. Tabulky Google nyní zobrazí graf bell curve na základě údajů v sešitu.

širší křivka zvonu znamená vyšší směrodatnou odchylku, zatímco vysoká a tenká křivka zvonu znamená nižší směrodatnou odchylku.

co je zvonová křivka a jak se používá v reálném životě?

zvonová křivka je typ rozdělení hodnot, ve kterém se datové body shlukují těsně k průměru.

to se obvykle používá v obchodních scénářích ke zjištění hodnot, které leží daleko od průměrné datové sady (stejně jako odlehlé hodnoty).

pokud například porovnáte výšky studentů ve třídě, uvidíte, že většina z těchto studentů je blízká průměru, přičemž někteří jsou nebo jsou na pravé straně zvonové křivky (což znamená, že jsou vyšší než průměrný student) a někteří jsou na levé straně zvonového grafu (což znamená, že jsou kratší než průměr.

pokud tedy vybíráte tým basketbalu, kde je výška výhodou, můžete se více zaměřit na studenty ve skupině outlier vpravo.

můžete použít grafy bell curve k zobrazení dat z investic do akcií, hodnot nemovitostí, tříd ve třídě, skóre recenzí a mnoha dalších datových skupin, které běžně konsolidují hodnoty blízké průměru.

to může pomoci při rozhodování o tom, kam bezpečně investovat nebo co dělá spravedlivou nabídku na nemovitost.

zejména jsou zvonové křivky užitečné pro porovnání skóre hodnocení, protože průměrné skóre často není střední hodnotou na stupnici.

například v systému hodnocení 1 až 10 se většina recenzí může pohybovat kolem 7, což definuje průměr. Alternativně, dávka recenzí, které vracejí značné množství odlehlých hodnot ze zvonové křivky, nemusí být považována za spolehlivou.

tento tutoriál popisuje, jak vytvořit graf křivek v Tabulkách Google. V případech použití v reálném světě je vytvoření grafu bell curve jen začátkem vizualizace a interpretace dat.

doufám, že jste našli tento návod užitečný!

další výukové programy Google Sheets, které se vám mohou líbit:

• jak vytvořit výsečový graf v Tabulkách Google
• jak vytvořit Histogram v Tabulkách Google
• jak vytvořit rozptylový graf v Tabulkách Google
• jak vytvořit řádkový graf v Tabulkách Google
• svícen v Tabulkách Google