fraktální umění představuje spojenectví umění a matematiky. Tato nedávná umělecká forma používá počítače k vytváření obrázků z matematických vzorců. Fraktální umění má často geometrický vzhled, složité vzory a množství detailů. Ale jak se vám jít o vytváření obrázků z matematických vzorců ?
co znamená „fraktál“?
v 70. letech objevil počítačový vědec Benoit Mandelbrot jeden z nejslavnějších fraktálních obrazů: Mandelbrotův set.

tento objev je umožněn vývojem počítače, zejména díky výpočetnímu výkonu. Probíhá také ve vědeckém kontextu vývoje teorie chaosu, která studuje dynamické jevy (turbulence, víry v tekutině, oscilace, tvar mraku atd.).
podobně se fraktální geometrie nachází ve tvarech přírody se složitými obrysy (sněhová vločka, list stromu, tvar mraků, víry,arborescence krevní sítě, tvar námořních pobřeží atd.), že bylo obtížné pochopit a modelovat s předchozími matematickými nástroji.

charakteristika fraktálních obrazů
fraktální dimenze
termín „fraktál“ označuje myšlenku necelého, frakčního rozměru. Až do šedesátých let matematika studovala rozložitelné objekty pomocí celočíselných rozměrů:
bod: dimenze 0
řádek: dimenze 1
plán: Dimenze 2
objem: dimenze 3
ale představte si list papíru. Představuje rovinu, proto má rozměr rovný 2. Pokud tento list zmačkáme, nyní zabírá objem (Rozměr 3), ale není to objem, protože nemůžeme zmačkaný list „naplnit“ materiálem, jako by se naplnil kontejner. Rozměr zmačkaného listu je tedy například mezi 2 a 3: 2.568. Fraktální rozměr ! Fraktální objekty tak mají složité, nepravidelné tvary, s konturami složenými a složenými na sebe.
vlastní podobnost
navzdory své složitosti vykazuje fraktální objekt podobné detaily. Zoomování uvnitř fraktálu ukazuje stejný celkový vzorec opakovaný v různých měřítcích a do nekonečna. Část je tedy podobná celku. Tato vlastnost se nazývá invariance měřítka.

typologie
fraktály podle opakování

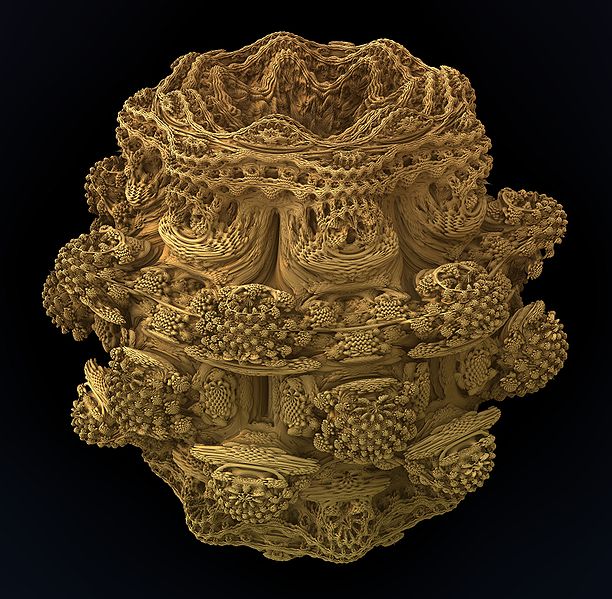
IFS, iterované funkční systémy



generování fraktálních obrazů,“jednoduchost plodí složitost“
konstrukce fraktálních obrazů je založena na použití algoritmu provedeného ve smyčce. Jedná se o iterativní proces opakující řadu jednoduchých operací.
fraktály opakováním
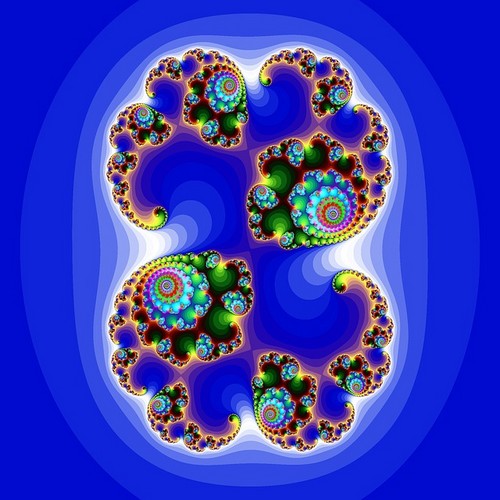
pro každý bod v prostoru jsou souřadnice bodu předány do rovnice. Výsledek je pak přiváděn zpět do stejné rovnice. Operace se provádí několikrát za sebou (iterace). Pak testujeme výsledek. Pokud výsledek má tendenci k nekonečnu, pak výchozí bod není v celku : je zbarven bíle. Pokud výsledek zůstane stabilní nebo periodický, pak je výchozí bod v celku : je zbarven černě. U bodů na hranici je obtížnější určit, zda jsou v sadě nebo venku. Poté je nutné provést více iterací. V závislosti na počtu iterací potřebných k určení bodu je barevný v různých odstínech. Body této hranice dávají fraktálu jeho komplikovaný a zamotaný vzhled.
k nakreslení Mandelbrotovy sady používáme komplexní čísla, z nichž každá představuje pixel v rovině. Pro každý bod provedeme následující rovnici: Zn + 1 = Zn2 + C, se Z0 = 0.
IFS, iterované funkční systémy
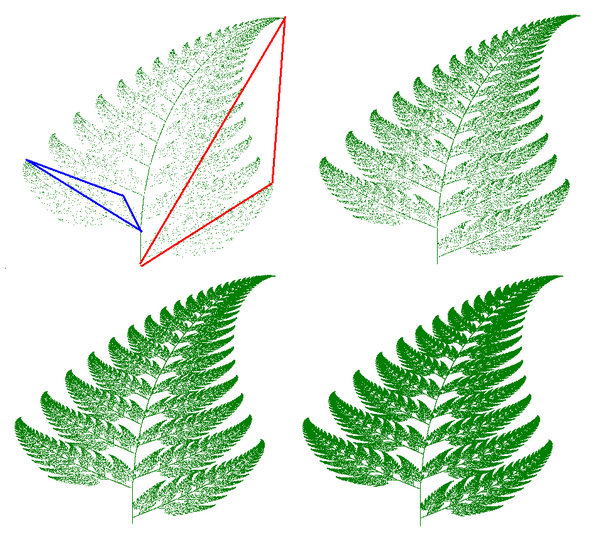
konstrukce obrazu se zde provádí samotným kopírováním. Ale s každou kopií kopírovaný obraz prochází geometrickou transformací (lineární transformace reprezentovaná v matematice lineární funkcí). Tyto transformace mohou být rotace, zploštění , stříhání … kopie jsou také kontrahovány před umístěním zpět na původní obrázek. Proces se opakuje, dokud se nevytvoří obraz.
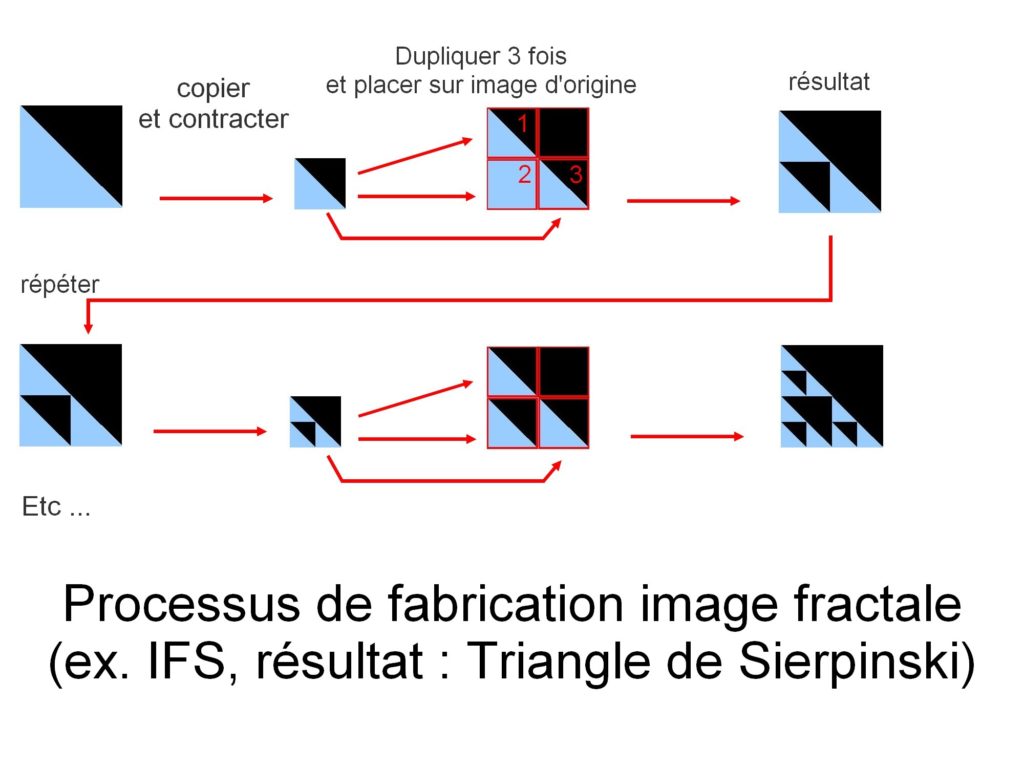
tento příklad má za následek obraz Sierpinského trojúhelníku.
dalším příkladem je generace sněhové vločky Koch.

IFS může snadno vytvářet obrazy připomínající přírodní objekty, jako jsou stromy, kapradiny atd.