ve zjednodušeném modelu popíšeme základy koaxiálních směrových spřáhel s jednou spojovací smyčkou. Princip je v podstatě stejný pro většinu ostatních směrových spojek.
koaxiální směrové spojky používají skutečnost, že směr elektrického pole (E-pole) mezi vnitřním a vnějším vodičem je stejný pro dopřednou a zpětnou vlnu. Avšak magnetické pole (H-pole) se směrem kolem vnitřního vodiče koaxiální linie má opačný směr otáčení pro dopřednou a reverzní vlnu. Ilustrujeme to na směrovém smyčkovém spojce odpovídajícím obr. 1.
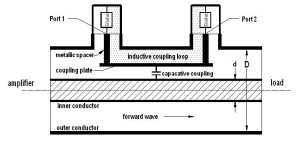
obr. 1
radiofrekvenční (rf) výkon proudící ze zesilovače do zátěže vede k radiálnímu elektrickému poli od vnitřního vodiče k vnějšímu vodiči (zemi) a kruhovému magnetickému poli mezi vnitřním a vnějším vodičem.
malá část elektrického pole se kondenzačně spojí od vnitřního vodiče ke spojovací desce spojovací smyčky. To vede k rf napětí této desky proti zemi a rf proudu, který protéká elektricky vedoucími kovovými rozpěrkami rovnoměrně přes dva 50 ohm odpory k zemi. Toto napětí, které vzniká v důsledku kapacitního spojení dopředné vlny, je stejné na obou portech a kladné. V následujícím textu nazýváme toto napětí +Vcap.
jak již bylo zmíněno, dopředná vlna také vytváří kruhové magnetické pole, které je svislé a ve směru hodinových ručiček orientované na směr šíření. Toto magnetické pole je umístěno kolem vnitřního vodiče a je vázáno vnějším vodičem. Malá část tohoto magnetického pole proniká do spojovací smyčky. Spojovací smyčka, sestávající ze spojovací desky, dvou kovových rozpěrek, dvou odporů a země mezi odpory, vytváří uzavřený obvod. Takzvaný magnetický tok přes spojovací smyčku indukuje proud v této uzavřené smyčce. Tento proud generuje kladné napětí +Vind na portu 1, protékající rezistorem na portu 1. Po průchodu tímto odporem, indukovaný proud Iind proudí podél země k rezistoru na portu 2. Směr tohoto proudu přes odpor na portu 2 je opačný k proudu přes odpor na portu 1. To vede k zápornému napětí-Vind na portu 2, předtím, než proud proudí zpět do spojovací desky.
pokud lze pomocí vhodné geometrie získat, že Vcap a Vind jsou stejné v amplitudě a fázi, bude to mít za následek dvojnásobné napětí na portu 1, Přidání v cap a V ind, zatímco přidání Vcap a-Vind na portu 2 povede k nulovému napětí. V tomto případě dopředná vlna spojuje část přepravované energie do portu 1, zatímco nic z toho se nespojí s portem 2.
pro reverzní vlnu se stejným směrem E-pole, ale opačným směrem h-pole je to naopak. Zde kapacitní a induktivní spojka přidává na portu 2, zatímco se navzájem zhasnou na portu 1.
na portu 1 měří jeden pouze proporcionální část dopředné vlny a na portu 2 pouze proporcionální část zpětné vlny. Směrová spojka tak může samostatně měřit dopřednou a reverzní vlnu.
v praxi nikdy nenajdete ideální podmínky, jak je právě popsáno. Pokud Vcap a Vind nejsou přesně stejné, dopředná vlna spojí malou část dopředného výkonu s portem 2 také. Podobně reverzní vlna spojí malou část s portem 1.
pokud například dopředná vlna spojuje jednu tisícinu přepravovaného výkonu do portu 1, má směrová spojka spojovací faktor -30 db. Zvažte další příklad, kde jeden měří -65 dB na portu 2 (místo ideálně-infinity dB) kvůli malé rozmanitosti mezi kapacitní a induktivní vazbou (i při ideálním přizpůsobení hlavní linie bez zpětné vlny). V tomto případě existuje rozdíl ve spojení portu 1 a portu 2 35 dB. Tento faktor se nazývá směrovost směrového spojky, která je v tomto příkladu 35 dB.
směrovost je měřítkem toho, jak dobře je kapacitní a induktivní vazba směrového vazebného prvku přizpůsobena amplitudě a fázi. Doporučujeme směrovost alespoň 30 dB, lepší 35 až 40 dB. Po našich vysvětleních o dvou napětích Vcap a Vind výše si můžete představit, že nejen geometrie spojovací smyčky, ale také kvalita a rovnost dvou 50 ohmových odporů mají silný vliv na směrovost směrového vazebného zařízení.
abychom to shrnuli, ukázali jsme, jak funguje směrový vazební člen a konkrétně, jak je dokonalý směrový vazební člen schopen samostatně měřit dopřednou a reverzní vlnu. Dále jsme definovali parametr směrovost směrového spřáhla a jeho napojení na nesymetrickou geometrii.