ruční výpočet tabulky ANOVA s Pythonem
pozadí

analýza rozptylu, obvykle označovaná jako ANOVA, je něco, co se často objevuje v úvodních třídách statistik. S dnešní technologií je snadné nechat počítač provádět všechny výpočty a stačí se podívat na hodnotu p na konci zaneprázdněné tabulky, jako je ta výše. V tomto článku projdu, co jsou tato čísla a co ANOVA vlastně dělá.
hlavní myšlenkou ANOVA je otestovat, zda existuje statisticky významný rozdíl v měřených prostředcích mezi podskupinami vzorku. Koncept se datuje kolem roku 1920 s britským statistikem jménem Ronald Fisher, který analyzoval obrovské množství údajů o výnosech plodin. Fisher použil ANOVU k prokázání významného rozdílu v průměrné hmotnosti brambor při použití různých hnojiv.
abych demonstroval ANOVU v současnosti, podívám se spíše na ceny vína než na váhy brambor. Údaje pro tento příklad pocházejí z Kaggle “ s Wine Review dataset, který obsahuje tisíce recenzí na láhve vína od WineEnthusiast. Filtroval jsem to na podmnožinu 3 000 recenzí vín ze Spojených států, Itálie a Francie (1 000 na zemi) a použiji ANOVA k testování, zda existuje statisticky významný rozdíl v průměrné ceně mezi zeměmi původu.
rychlý graf distribuce cen podle zemí ukazuje tři docela podobné distribuce, přičemž většina cen se pohybuje kolem $ 25 za láhev.

Vezmeme-li v úvahu průměr každé země, vidíme, že Francie má v průměru nejdražší víno, následuje Itálie a nakonec USA. Otázkou však je, je to skutečný rozdíl v ceně mezi zeměmi, nebo by to mohlo být jen kvůli variaci vzorku? To je místo, kde ANOVA přichází do hry.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
čtyři kroky k Anově jsou:
1. Formulujte hypotézu
2. Nastavte úroveň významnosti
3. Vypočítejte F-statistiku
4. Použijte F-statistiku k odvození hodnoty p
5. Porovnejte hodnotu p a úroveň významnosti a rozhodněte se, zda odmítnout nulovou hypotézu
formulujte hypotézy
stejně jako u téměř všech testů statistické významnosti začíná ANOVA formulováním nulové a alternativní hypotézy. V tomto příkladu jsou hypotézy následující:
nulová hypotéza (H0): Neexistuje žádný rozdíl v průměrné ceně vína mezi těmito třemi zeměmi; všechny jsou stejné.
alternativní hypotéza (H1): průměrná cena vína není mezi těmito třemi zeměmi stejná.
Poznámka: Toto je omnibusový test, což znamená, že pokud jsme schopni odmítnout nulovou hypotézu, řekne nám, že někde mezi těmito zeměmi existuje statisticky významný rozdíl, ale neřekne nám, kde je.
nastavte úroveň významnosti
úroveň významnosti nebo alfa je pravděpodobnost odmítnutí naší nulové hypotézy, když skutečně platí. Jinými slovy je to pravděpodobnost chyby typu I.
Obvykle byste měli zvážit náklady na provedení chyby typu I vs. typu II, abyste určili nejlepší alfa pro experiment, ale pro tento příklad hračky použiji standard .05 pro naši hodnotu α.
Vypočítejte F-statistiku
F-statistika je jednoduše poměr rozptylu mezi prostředky vzorků k rozptylu v rámci prostředků vzorku. Pro tento test ANOVA se podíváme na to, jak daleko je průměrná cena vína v každé zemi od celkové průměrné ceny, a vydělíme to tím, kolik rozdílů v ceně je v rámci distribuce vzorků v každé zemi. F-statistický vzorec je níže, což může vypadat komplikovaně, dokud jej nerozebereme.
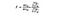
SSB = součet čtverců mezi skupinami. Toto je součet čtvercového rozdílu mezi průměrem každé skupiny a celkovým průměrem krát počet prvků na skupinu. V tomto příkladu vezmeme průměr ceny vína v každé zemi, odečteme ji od celkového průměru, odečteme rozdíl a vynásobíme 1 000 (počet datových bodů na zemi).
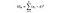
SSW = součet čtverců ve skupinách. Toto je součet čtvercového rozdílu mezi průměrem skupiny a každou hodnotou ve skupině. Pro Francii bychom vzali průměrnou cenu francouzského vína, poté odečetli a umocnili rozdíl pro každou láhev francouzského vína z tisíců datových bodů v této skupině.
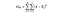
DoFB = stupně volnosti mezi skupinami, jednoduše počet skupin minus 1. Máme tři různé země, které porovnáváme, takže stupně volnosti jsou zde 2.
DoFW = stupně volnosti ve skupinách, jednoduše počet datových bodů minus počet skupin. Máme 3 000 datových bodů a tři různé země, takže pro tento příklad je to 2 997.
vydělením součtu čtverců pro skupinu podle jejích stupňů volnosti získáte střední čtverce pro tuto skupinu a statistika F je jen poměr středních čtverců mezi středními čtverci uvnitř.
níže ručně vypočítám tyto hodnoty v Pythonu a skončím s F-statistikou ~4.07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
pomocí F-statistiky vypočítáme p-hodnotu
jakmile máme naši F-statistiku, zapojíme ji do F-distribuce, abychom získali P-hodnotu. Tabulku pro tyto hodnoty najdete v zadní části jakékoli statistiky nebo existují mnohem jednodušší online kalkulačky, které to udělají za vás. S našimi specifickými stupni volnosti, F-Statistika 4,07 dává p-hodnotu .0172.

Porovnejte hodnotu p a úroveň významnosti a rozhodněte se, zda odmítnout nulovou hypotézu
naše hodnota p znamená, že za předpokladu, že nulová hypotéza (všechny země mají stejnou střední cenu vína)je pravdivá, existuje zhruba 1.7% šance vidět data, která máme, pouhou náhodou vzorkování. Stanovením naší úrovně významnosti nebo alfa na 5% před tím vším jsme řekli, že bychom byli ochotni přijmout 5% šanci odmítnout null, pokud je to pravda. Vzhledem k tomu, že naše hodnota p je pod naší předem stanovenou úrovní významnosti, můžeme nulovou hypotézu odmítnout a říci, že existuje statisticky významný rozdíl v průměrné ceně vína mezi zeměmi.
nezapomeňte, že ANOVA je omnibusový test, což znamená, že jsme schopni odmítnout null, víme, že existuje rozdíl mezi průměrnými cenami vína mezi zeměmi, ale ne přesně tam, kde. Abychom zjistili, kde je rozdíl, provedli bychom testy hypotéz mezi dvěma zeměmi najednou.
Automatická ANOVA
stejně jako u většiny věcí v životě má Python intuitivní řešení pro vedení ANOVA s knihovnou statsmodel. Níže uvedený kód provádí všechny výpočty v tomto článku a vydává souhrnnou tabulku s F-statistikou a p-hodnotou.

Díky za přečtení, úplný kód a data najdete na mé stránce GitHub.