která je nejlepší měrnou jednotkou pro úhly — otáčky, stupně nebo radiány?
otáčky
zřídka se naučíme používat nejjednodušší, nejpřirozenější měrnou jednotku pro geometrické úhly, otáčky (rev). Další názvy pro tuto jednotku jsou full circle, turn, full turn a rotation(rot). To jsou všechna dobrá jména a všechna znamenají totéž.
1 celý kruh = 1 ot / min = 1 ot / min = 1 ot / min = 360°
stupně
na základní škole se dozvídáme, že úhly se měří ve stupních (°).
1 celý kruh = 360°
radiány
ve třídách trigonometrie a počtu na střední škole se dozvídáme, že matematici dávají přednost radiánům (rad).
1 full circle = 2π rad
Poznámka: Pokud jste se ještě nenaučili o radiánech ve škole, můžete ignorovat radiány ve všem níže.
porovnání otáček, stupňů a radiánů
porovnejme otáčky a stupně (a radiány).
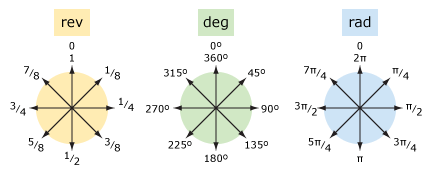
| slova | rev | deg | rad |
|---|---|---|---|
| žádný obrat | 0 | 0° | 0 |
| čtvrt otáčky | 1/4 | 90° | π/2 |
| půl otáčky | 1/2 | 180° | π |
| tříčtvrteční obrat | 3/4 | 270° | 3π/2 |
| plný obrat | 1 | 360° | 2π |
| dvanáctá zatáčka | 1/12 | 30° | π/6 |
| osmé kolo | 1/8 | 45° | π/4 |
| šestá zatáčka | 1/6 | 60° | π/3 |
| pátá zatáčka | 1/5 | 72° | 2π/5 |
| třetí zatáčka | 1/3 | 120° | 2π/3 |
| dvě zatáčky | 2 | 720° | 4π |
| tři otáčky | 3 | 1080° | 6π |
Chcete-li převést z otáček na stupně, vynásobte 360. Chcete-li převést ze stupňů na otáčky, vydělte 360.
při použití stupňů často pracujete s celými čísly, ale při použití otáček (nebo radiánů) často pracujete se zlomky(nebo desetinnými místy). Ruční výpočty jsou někdy jednodušší, když používáte otáčky, ale někdy jednodušší, když používáte stupně. Je dobré vědět obojí.
otáčky (otáčky) jsou racionálnější a přirozenější měrnou jednotkou než stupně. Získáte hlubší pochopení úhlů, pokud přemýšlíte o otáčkách spíše než o stupních. Úhel je zásadněji rozdělení kruhu spíše než součet stupňů. Například pravý úhel je zásadněji čtvrtina kruhu spíše než součet 90 stupňů.
rozdělíme kružnici na n stejné sektory (viz obrázek níže). Úhel každého sektoru je 1 / n rev = 360 / n° = 2π / n rad. Je snazší to pochopit, pokud přemýšlíte spíše o otáčkách než o stupních (nebo radiánech).

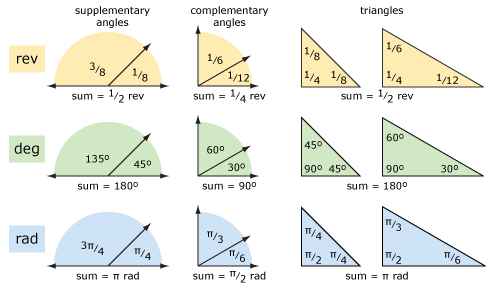
podívejme se na základní geometrii pomocí otáček a stupňů (a radiánů). Níže uvedený diagram ukazuje doplňkové úhly, doplňkové úhly a trojúhelníky. Pojmy jsou jasnější, pokud přemýšlíte spíše o revolucích než o stupních. Aritmetika může být jednodušší pomocí stupňů, pokud máte potíže s přidáním a odečtením zlomků.
podívejme se na mnohoúhelníky (viz obrázek níže). Pro pravidelný mnohoúhelník s n stranami je vnější úhel 1 / n ot = 360 / n° = 2π / n rad. Je snazší to pochopit, pokud přemýšlíte spíše o otáčkách než o stupních (nebo radiánech). Vnitřní úhel je doplňkem vnějšího úhlu.

výuka revolucí, stupňů a radiánů
myslím, že by bylo dobré, kdyby učitelé zavedli revoluce (obraty) současně s zaváděním stupňů. To pomůže studentům pochopit úhly na zásadnější úrovni, méně závislé na libovolném magickém čísle 360. Učitelé již zavádějí obecný koncept otáček (otáček), když říkají věci jako “ celý kruh je 360°“, ale mohou tento koncept numericky přesnější slovy „Plná zatáčka je 360°, polovina otáčky je 180°, čtvrtina otáčky je 90° a osmá zatáčka je 45°“ nebo psaní „1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90° a 1/8 rev = 45°“. Studenti by měli občas procvičovat několik výpočtů pomocí otáček (otáček) spíše než stupňů. Samozřejmě, studenti budou muset trávit většinu času učením se počítat s tituly (a později radiány), protože to je standard.
úhly v trigonometrii a počtu
nakonec se podívejme na pokročilejší matematiku: trigonometrii a počet.
můžeme uvažovat o použití otáček s trigonometrickými funkcemi (sinus, kosinus, tečna). Například místo toho, abychom řekli cos (60°) = 1/2 nebo cos (π/3) = 1/2 pomocí radiánů, můžeme říci cos (1/6) = 1/2 pomocí otáček. To však není praktické, protože při hodnocení trigonometrických funkcí závisíme na kalkulačkách a kalkulačky mají obvykle pouze režimy DEG a RAD, nikoli režim REV.
když jdeme na hlubší úrovně matematiky, jako je počet a matematická analýza, ukazuje se, že radiány jsou nejracionálnější a nejpřirozenější jednotky. Zvažte například tuto základní rovnici: limit sin (x)/x, když se x blíží 0, je přesně 1. Tato rovnice by nebyla tak elegantní, kdybychom použili jinou jednotku než radiány.