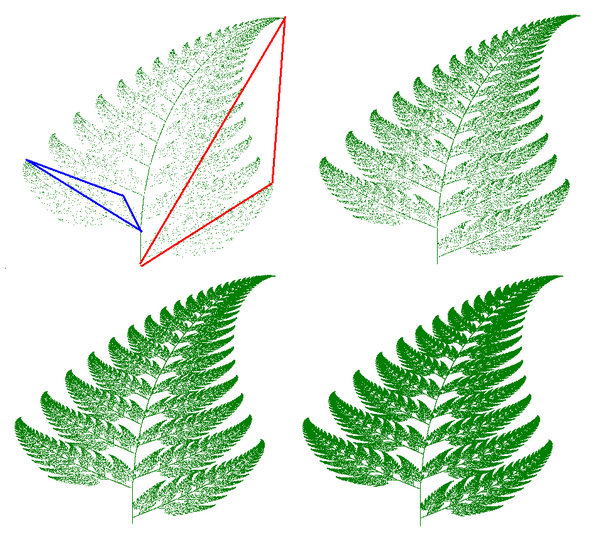
L’arte frattale rappresenta l’alleanza tra arte e matematica. Questa forma d’arte recente utilizza i computer per creare immagini da formule matematiche. L’arte frattale ha un aspetto spesso geometrico, motivi intricati e una ricchezza di dettagli. Ma come si fa a creare immagini da formule matematiche ?
- Prima di tutto, cosa significa “Frattale”?
- Caratteristiche delle immagini frattali
- La dimensione frattale
- Auto-somiglianza
- Tipologia
- Frattali da ricorrenza
- IFS, iterato funzioni dei sistemi
- Generazione di immagini frattali,”Semplicità genera complessità”
- Frattali per ricorrenza
- IFS, iterated functions systems
Prima di tutto, cosa significa “Frattale”?
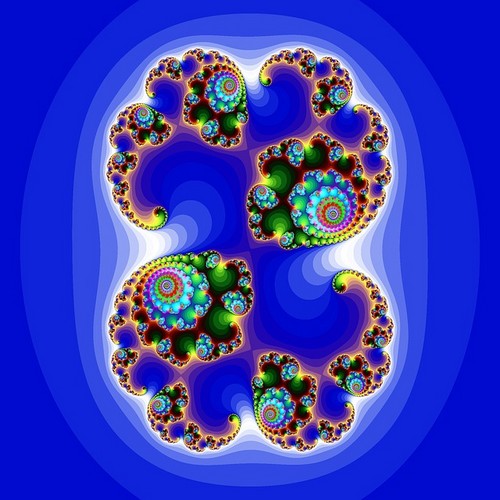
Nel 1970, l’informatico Benoit Mandelbrot scoprì una delle immagini frattali più famose: il set di Mandelbrot.

Questa scoperta è resa possibile dallo sviluppo del computer, in particolare grazie alla potenza di calcolo. Si svolge anche nel contesto scientifico dello sviluppo della teoria del Caos che studia i fenomeni dinamici (turbolenza, vortici in un fluido, oscillazione, forma di nuvola, ecc.).
Allo stesso modo, la geometria frattale si trova nelle forme della natura con contorni complessi (fiocco di neve, foglia di un albero, forma di nuvole, vortici, arborescenza della rete sanguigna, forma delle coste marittime, ecc.) che era difficile da capire, e da modellare con i precedenti strumenti matematici.

Caratteristiche delle immagini frattali
La dimensione frattale
Il termine “frattale” si riferisce all’idea di una dimensione frazionaria non intera. Fino al 1960, la matematica studiata scomponibile oggetti utilizzando integer dimensioni:
un punto: dimensione 0
una riga: dimensione 1
un piano: dimensione 2
un volume: dimensione 3
Ma immaginate un foglio di carta. Rappresenta un piano, quindi ha una dimensione pari a 2. Se accartocciamo questo foglio, ora occupa un volume (dimensione 3), ma non è un volume perché non possiamo “riempire” il foglio accartocciato con un materiale come si riempirebbe un contenitore. La dimensione del foglio accartocciato è quindi compresa tra 2 e 3: 2.568 per esempio. Una dimensione frattale ! Gli oggetti frattali hanno così forme complesse e irregolari, con contorni piegati e piegati su se stessi.
Auto-somiglianza
Nonostante la sua complessità, un oggetto frattale presenta dettagli simili. Lo zoom all’interno di un frattale mostra lo stesso schema generale ripetuto a scale diverse e all’infinito. Una parte è quindi simile al tutto. Questa proprietà è chiamata invarianza di scala.

Tipologia
Frattali da ricorrenza

IFS, iterato funzioni dei sistemi



Generazione di immagini frattali,”Semplicità genera complessità”
La costruzione di immagini frattali si basa sull’uso di algoritmi eseguiti in un ciclo. È un processo iterativo che ripete una serie di semplici operazioni.
Frattali per ricorrenza
Per ogni punto nello spazio, le coordinate del punto vengono passate in un’equazione. Il risultato viene quindi reinserito nella stessa equazione. L’operazione viene eseguita più volte di seguito (iterazioni). Quindi testiamo il risultato. Se il risultato tende all’infinito, allora il punto di partenza non è nel tutto : è colorato di bianco. Se il risultato rimane stabile o periodico, il punto di partenza è nel complesso : è colorato di nero. Per i punti sul confine, è più difficile determinare se sono nel set o all’esterno. È quindi necessario eseguire più iterazioni. A seconda del numero di iterazioni necessarie per determinare il punto, è colorato in diverse tonalità. I punti di questo bordo danno al frattale il suo aspetto complicato e aggrovigliato.
Per disegnare il set di Mandelbrot, usiamo numeri complessi che rappresentano ciascuno un pixel sul piano. Eseguiamo la seguente equazione per ogni punto: Zn + 1 = Zn2 + C, con Z0 = 0.
IFS, iterated functions systems
La costruzione dell’immagine viene eseguita qui copiando se stessa. Ma con ogni copia, l’immagine copiata subisce una trasformazione geometrica (una trasformazione lineare rappresentata in matematica da una funzione lineare). Queste trasformazioni possono essere rotazioni, appiattimento, taglio … Le copie vengono anche contratte prima di essere rimesse sull’immagine originale. Il processo viene ripetuto fino a formare un’immagine.
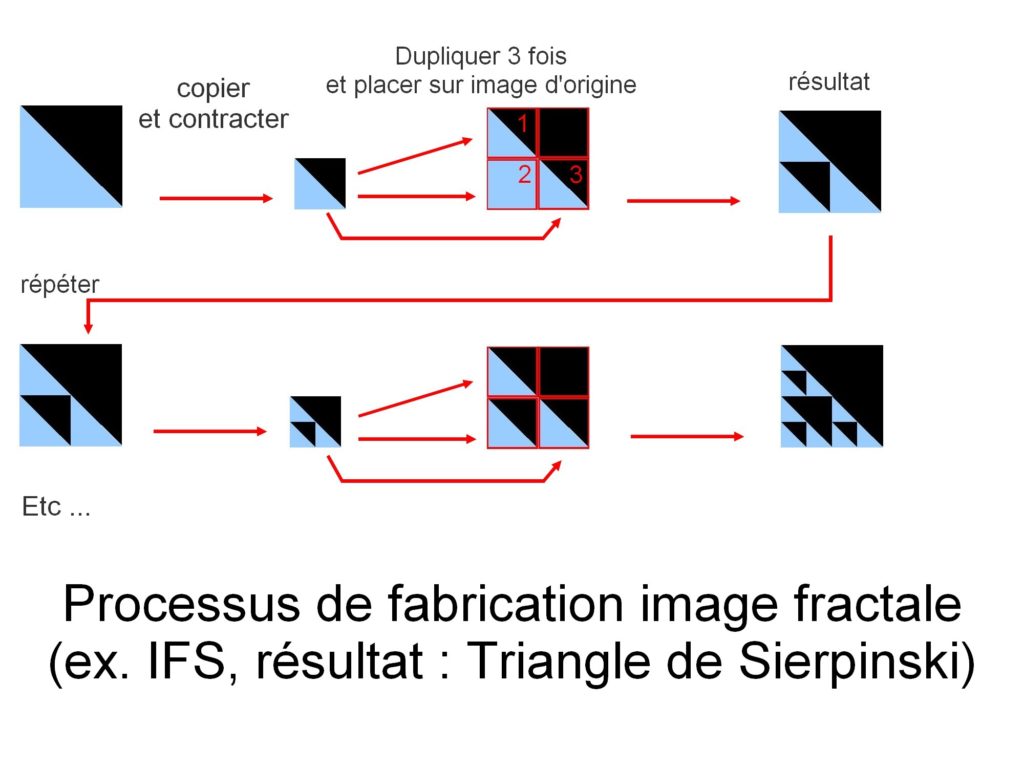
Questo esempio produce l’immagine del triangolo di Sierpinski.
Un altro esempio è la generazione del fiocco di neve Koch.

IFS può facilmente produrre immagini che ricordano oggetti naturali, come alberi, felci, ecc.