Manualmente il Calcolo di una Tabella ANOVA con Python
Sfondo

Analisi della varianza, in genere indicato come ANOVA, è qualcosa che spesso sorvolata in introduttivo alla statistica classi. Con la tecnologia di oggi, è facile lasciare che il computer faccia tutti i calcoli e basta guardare il valore p alla fine di una tabella dall’aspetto occupato come quella sopra. In questo articolo, esaminerò quali sono questi numeri e cosa sta effettivamente facendo ANOVA.
L’idea principale alla base di ANOVA è quella di verificare se esiste una differenza statisticamente significativa nella media misurata tra i sottogruppi di un campione. Il concetto risale a circa 1920 con uno statistico britannico di nome Ronald Fisher, che stava analizzando enormi quantità di dati sui raccolti. Fisher ha usato ANOVA per dimostrare che c’era una differenza significativa nel peso medio delle patate quando venivano usati diversi fertilizzanti.
Per dimostrare ANOVA ai giorni nostri, guarderò i prezzi del vino piuttosto che i pesi delle patate. I dati di questo esempio provengono dal set di dati Wine Review di Kaggle, che contiene migliaia di recensioni su bottiglie di vino di WineEnthusiast. L’ho filtrato fino a un sottoinsieme di recensioni 3,000 per vini provenienti da Stati Uniti, Italia e Francia (1,000 per paese) e userò ANOVA per verificare se esiste una differenza statisticamente significativa nel prezzo medio tra i paesi di origine.
Un breve grafico della distribuzione dei prezzi per paese mostra tre distribuzioni piuttosto simili, con la maggior parte dei prezzi intorno a $25 a bottiglia.

Prendendo la media di ogni paese, vediamo che la Francia è il vino più costoso in media, seguita da Italia e infine la parte di NOI. Ma la domanda è: si tratta di una vera differenza di prezzo tra i paesi o potrebbe essere dovuta solo alla variazione del campione? Questo è dove ANOVA entra in gioco.
wine_df.groupby('country').mean()country
France 37.242
Italy 35.286
US 33.776
Name: price, dtype: float64
I quattro passi per ANOVA sono:
1. Formulare un’ipotesi
2. Impostare un livello di significatività
3. Calcola una statistica F
4. Utilizzare la statistica F per ricavare un valore p
5. Confronta il p-value e il livello di significatività per decidere se rifiutare o meno l’ipotesi nulla
Formulare un’ipotesi
Come con quasi tutti i test di significatività statistica, ANOVA inizia con la formulazione di un’ipotesi nulla e alternativa. Per questo esempio, le ipotesi sono le seguenti:
Ipotesi nulla (H0): Non vi è alcuna differenza nel prezzo medio del vino tra i tre paesi; sono tutti uguali.
Ipotesi alternativa (H1): Il prezzo medio del vino non è lo stesso tra i tre paesi.
Nota, questo è un test omnibus, il che significa che se siamo in grado di rifiutare l’ipotesi nulla ci dirà che esiste una differenza statisticamente significativa da qualche parte tra questi paesi, ma non ci dirà dove si trova.
Imposta un livello di significatività
Il livello di significatività, o alfa, è la probabilità di rifiutare la nostra ipotesi nulla quando è effettivamente vera. In altri termini, è la probabilità di commettere un errore di tipo I.
In genere, si dovrebbero pesare i costi di creazione di un errore di tipo I rispetto a un errore di tipo II per determinare il miglior alfa per un esperimento, ma per questo esempio di giocattolo userò solo lo standard .05 per il nostro valore α.
Calcola una statistica F
La statistica F è semplicemente un rapporto tra la varianza tra i mezzi dei campioni e la varianza all’interno dei mezzi del campione. Per questo test ANOVA, vedremo quanto il prezzo medio del vino di ciascun paese è lontano dal prezzo medio complessivo e dividendolo per quanta variazione di prezzo c’è all’interno della distribuzione del campione di ciascun paese. La formula F-statistica è sotto, che può sembrare complicata fino a quando non la scomponiamo.
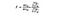
SSB = Somma di quadrati tra gruppi. Questa è la somma della differenza al quadrato tra la media di ciascun gruppo e la media complessiva per il numero di elementi per gruppo. Per questo esempio, prendiamo la media del prezzo del vino di ciascun paese, la sottraiamo dalla media complessiva, quadriamo la differenza e moltiplichiamo per 1.000 (il numero di punti dati per paese).
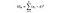
SSW = Somma di quadrati all’interno di gruppi. Questa è la sommatoria della differenza al quadrato tra la media del gruppo e ogni valore nel gruppo. Per la Francia, prendiamo il prezzo medio del vino francese, quindi sottraiamo e quadriamo la differenza per ogni bottiglia di vino francese dei mille punti dati in quel gruppo.
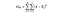
DoFB = Gradi di libertà tra gruppi, semplicemente il numero di gruppi meno 1. Abbiamo tre diversi paesi che stiamo confrontando, quindi i gradi di libertà qui sono 2.
DoFW = Gradi di libertà all’interno dei gruppi, semplicemente il numero di punti dati meno il numero di gruppi. Abbiamo 3.000 punti dati e tre paesi diversi, quindi questo è 2.997 per questo esempio.
Dividendo la somma dei quadrati per un gruppo per i suoi gradi di libertà si ottengono i quadrati medi per quel gruppo, e la statistica F è solo un rapporto tra i quadrati medi tra i quadrati medi all’interno.
Di seguito calcolo manualmente questi valori in Python e finisco con una statistica F di ~4.07.
Sum of Squares Between: 6039.73
Sum of Squares Within: 2226089.55
Degrees of Freedom for SSB: 2
Degrees of Freedom for SSW: 2997
F-Statistic: 4.06567
Usando la statistica F, calcola un valore p
Una volta che abbiamo la nostra statistica F, la colleghiamo a una distribuzione F per ottenere un valore p. Puoi trovare una tabella per questi valori nella parte posteriore di qualsiasi libro di statistiche o ci sono calcolatori online molto più facili che lo faranno per te. Con i nostri specifici gradi di libertà, una statistica F di 4.07 produce un valore P.0172.

Confrontare il p-value e livello di significatività a decidere se o non rifiutare l’ipotesi nulla
Il p-value indica che l’ipotesi l’ipotesi nulla (tutti i paesi hanno lo stesso prezzo medio del vino) è vero, c’è circa 1.7% di possibilità di vedere i dati che abbiamo per pura possibilità di campionamento. Impostando il nostro livello di significatività, o alfa, al 5% prima di tutto questo, abbiamo detto che saremmo disposti ad accettare una probabilità del 5% di rifiutare il null quando è vero. Poiché il nostro valore p è inferiore al nostro livello di significatività predeterminato, possiamo rifiutare l’ipotesi nulla e dire che esiste una differenza statisticamente significativa nel prezzo medio del vino tra i paesi.
Ricorda che ANOVA è un test omnibus, nel senso che poiché siamo in grado di rifiutare il null sappiamo che esiste una differenza tra i prezzi medi del vino tra i paesi, ma non esattamente dove. Per trovare dove si trova la differenza, condurremmo quindi test di ipotesi tra due paesi alla volta.
ANOVA automatica
Come con la maggior parte delle cose nella vita, Python ha una soluzione intuitiva per condurre ANOVA con la libreria statsmodel. Il codice seguente esegue tutti i calcoli in questo articolo e produce una tabella riassuntiva completa di F-statistica e p-valore.

Grazie per la lettura, il codice completo e i dati possono essere trovati sulla mia pagina GitHub.