Qual è la migliore unità di misura per angoli — giri, gradi o radianti?
Rivoluzioni
Raramente impariamo ad usare l’unità di misura più semplice e naturale per gli angoli geometrici, la rivoluzione (rev). Altri nomi per questa unità sono full circle, turn, full turn e rotation (rot). Questi sono tutti buoni nomi e significano tutti la stessa cosa.
1 cerchio completo = 1 giro = 1 giro = 1 marciume = 360°
Gradi
Nella scuola elementare, apprendiamo che gli angoli sono misurati in gradi (°).
1 cerchio completo= 360°
Radianti
Nelle classi di trigonometria e calcolo delle scuole superiori, apprendiamo che i matematici preferiscono i radianti (rad).
1 full circle = 2π rad
Nota: Se non hai ancora imparato a conoscere i radianti a scuola, puoi ignorare i radianti in tutto ciò che segue.
Confronto di rivoluzioni, gradi e radianti
Confrontiamo rivoluzioni e gradi (e radianti).
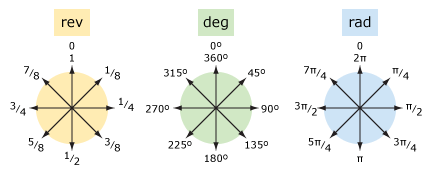
| parole | ap | deg | rad |
|---|---|---|---|
| non girare | 0 | 0° | 0 |
| quarto di giro | 1/4 | 90° | π/2 |
| mezzo giro | 1/2 | 180° | π |
| tre quarti di giro | 3/4 | 270° | 3π/2 |
| giro completo | 1 | 360° | 2π |
| dodicesimo turno | 1/12 | 30° | π/6 |
| ottavo turno | 1/8 | 45° | π/4 |
| sesto turno | 1/6 | 60° | π/3 |
| quinto turno | 1/5 | 72° | 2π/5 |
| terzo turno | 1/3 | 120° | 2π/3 |
| due giri | 2 | 720° | 4π |
| tre giri | 3 | 1080° | 6π |
Per convertire da giri a gradi, moltiplicare per 360. Per convertire da gradi a giri, dividere per 360.
Quando si usano i gradi si lavora spesso con numeri interi, ma quando si usano giri (o radianti) si lavora spesso con frazioni (o decimali). Calcoli a mano sono a volte più facile quando si utilizzano le rivoluzioni, ma a volte più facile quando si utilizzano gradi. È bello sapere in entrambi i modi.
Le rivoluzioni (spire) sono un’unità di misura più razionale e naturale dei gradi. Otterrai una comprensione più profonda degli angoli se pensi alle rivoluzioni piuttosto che ai gradi. Un angolo è più fondamentalmente una suddivisione di un cerchio piuttosto che una somma di gradi. Ad esempio, un angolo retto è più fondamentalmente un quarto di cerchio piuttosto che una somma di 90 gradi.
Dividiamo il cerchio in n settori uguali (vedi diagramma sotto). L’angolo di ogni settore è 1 / n rev = 360/n° = 2π / n rad. È più facile capirlo se pensi alle rivoluzioni piuttosto che ai gradi (o ai radianti).

Diamo un’occhiata ad alcune geometrie di base usando giri e gradi (e radianti). Lo schema seguente mostra angoli supplementari, angoli complementari e triangoli. I concetti sono più chiari se pensi alle rivoluzioni piuttosto che ai gradi. L’aritmetica può essere più facile usando i gradi se hai problemi ad aggiungere e sottrarre frazioni.
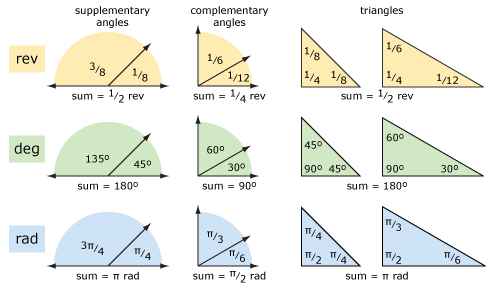
Diamo un’occhiata ai poligoni (vedi diagramma sotto). Per un poligono regolare con n lati, l’angolo esterno è 1 / n rev = 360/n° = 2π / n rad. È più facile capirlo se pensi alle rivoluzioni piuttosto che ai gradi (o ai radianti). L’angolo interno è il supplemento dell’angolo esterno.

Insegnare Rivoluzioni, gradi e radianti
Penso che sarebbe bene se gli insegnanti introducessero rivoluzioni (turni) nello stesso momento in cui introducono gradi. Ciò aiuterà gli studenti a comprendere gli angoli a un livello più fondamentale, meno dipendente dal numero magico arbitrario 360. Gli insegnanti già introducono il concetto generale di giri (giri) quando dicono cose come ” un cerchio completo è 360°”, ma possono rendere il concetto più preciso numericamente dicendo” un giro completo è 360°, un mezzo giro è 180°, un quarto di giro è 90° e un ottavo giro è 45° “o scrivendo”1 rev = 360°, 1/2 rev = 180°, 1/4 rev = 90° e 1/8 rev = 45°”. Gli studenti dovrebbero occasionalmente esercitarsi a fare alcuni calcoli usando le rivoluzioni (giri) piuttosto che i gradi. Naturalmente, gli studenti dovranno trascorrere la maggior parte del loro tempo imparando a calcolare con gradi (e più tardi, radianti), perché questo è lo standard.
Angoli in trigonometria e calcolo
Infine, diamo un rapido sguardo alla matematica più avanzata: trigonometria e calcolo.
Possiamo considerare l’utilizzo di giri con funzioni trigonometriche (seno, coseno, tangente). Ad esempio, invece di dire cos(60°) = 1/2 o cos(π/3) = 1/2 usando i radianti, potremmo voler dire cos(1/6) = 1/2 usando i giri. Ma questo non è pratico perché dipendiamo dalle calcolatrici per valutare le funzioni trigonometriche, e le calcolatrici in genere hanno solo modalità DEG e RAD, non la modalità REV.
Quando andiamo a livelli più profondi della matematica, come il calcolo e l’analisi matematica, si scopre che i radianti sono le unità più razionali e naturali. Ad esempio, considera questa equazione fondamentale: il limite di sin(x)/x quando x si avvicina a 0 è esattamente 1. Questa equazione non sarebbe così elegante se usassimo un’unità diversa dai radianti.